filmov
tv
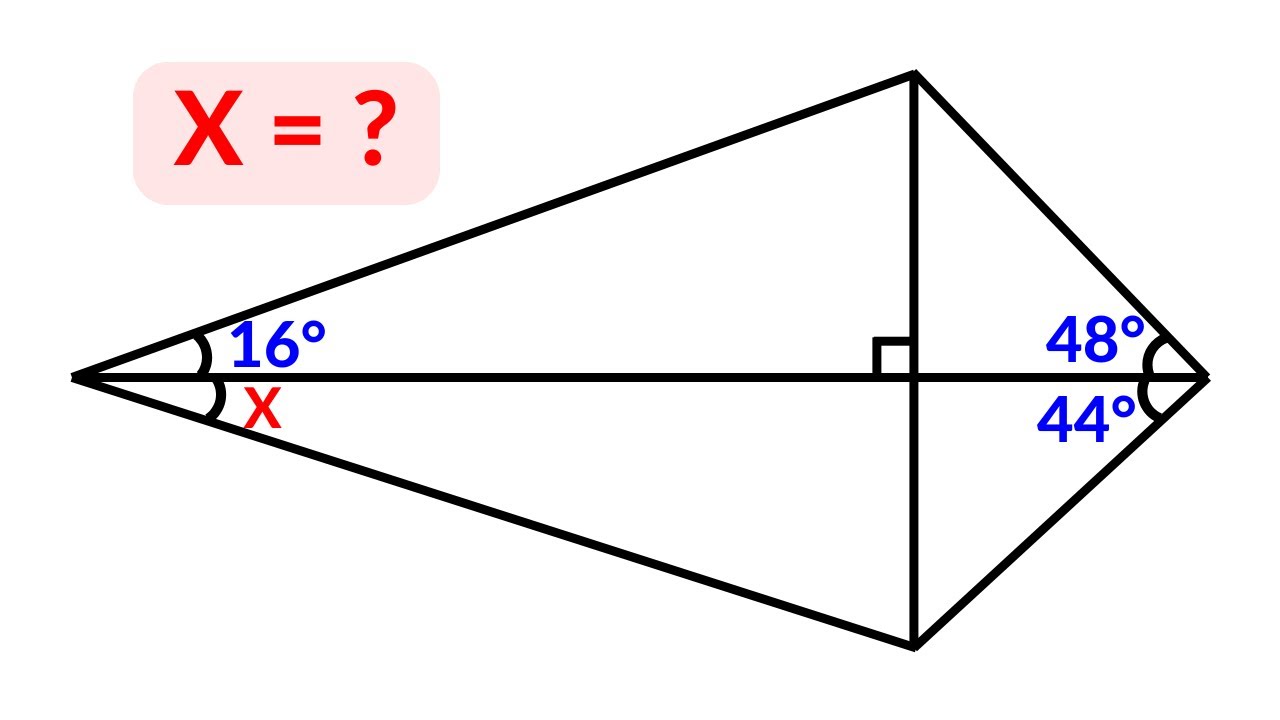
Find the angle X | Norway Math Olympiad Problem
Показать описание
GET MY EBOOKS
•••••••••••••••••••••••
OTHER CHAPTERS : COMING SOON.....
--------------------------------------------------------------------------------
Join the channel to become a member
•••••••••••••••••••••••
OTHER CHAPTERS : COMING SOON.....
--------------------------------------------------------------------------------
Join the channel to become a member
Can You Find Angle X? | Geometry Challenge!
Can you find the Angle X? | Quick & Simple Tutorial
Can you Find Angle X? Step-by-step Explanation
Challenge Question: Can you find the Angle X?| Step-by-Step Explanation
Geometry | Find the angle #math #tutor #mathtrick #learning #geometry #angles #x
Can you find the angle X? | (Justify your answer) | #math #maths | #geometry
Find the measure of three angles by determining the value of x
Calculate angle X in a 5-sided irregular Polygon | Learn how to Solve this Geometry problem Quickly
Can you find Angle X? Justify your answer! | Quick & Simple Explanation
Can you calculate Angle X in 1 Minute? | Step-by-Step Tutorial
Can You Find Angle X? Geometry video.
Find the angle X | How to Solve this Tricky Geometry problem Quickly
Can You Find Angle X? | Quick & Simple Explanation
Finding the Missing Angle of a Triangle: A Step-by-Step Guide | Triangles | Math with Mr. J
Geometry Puzzle || Find angle x || Puzzled
Learn to find the missing angles for a triangle using inverse trig functions
Topper Vs Back bencher | Exterior Angle Property #shorts #youtubeshorts #ashortaday #viralmaths #fun
Can you find the angle X? | Two isosceles triangles | [Step-by-step explanation]
Can you calculate the angle X? | (Justify your answer) | #math #maths | #geometry
Geometry Problem | Finding the Missing Angle | SAT Prep | Math Problem
Angles of Triangle: Sum of Interior Angles and Exterior Angle Theorem by @MathTeacherGon
How To Find X and Y with Parallel Angles -Alternate Interior Angles and Supplementary
Find the Value of Angle X in this Triangle | Fast & Easy Tutorial
Can you find the angle X? | Triangles in a quadrilateral | (Step-by-step explanation) | #math #maths
Комментарии
 0:08:44
0:08:44
 0:04:44
0:04:44
 0:04:54
0:04:54
 0:08:05
0:08:05
 0:00:16
0:00:16
 0:09:50
0:09:50
 0:01:09
0:01:09
 0:03:17
0:03:17
 0:08:03
0:08:03
 0:04:52
0:04:52
 0:01:50
0:01:50
 0:06:42
0:06:42
 0:05:12
0:05:12
 0:05:14
0:05:14
 0:07:21
0:07:21
 0:06:40
0:06:40
 0:00:13
0:00:13
 0:04:02
0:04:02
 0:07:15
0:07:15
 0:00:44
0:00:44
 0:07:00
0:07:00
 0:05:00
0:05:00
 0:04:53
0:04:53
 0:08:26
0:08:26