filmov
tv
Find the Value of Angle X in this Triangle | Fast & Easy Tutorial

Показать описание
Finding Missing Angles Vertical and Supplementary Angles
How To Find The Value Of an Angle
Find the measure of three angles by determining the value of x
Finding the value of x using supplementary angles - Free Math Videos
Find the Value of x, and the Missing Angle Measures
Complementary Angles & Supplementary Angles | Math with Mr. J
Finding the Value of Unknown Angles - Geometry
Angles of Triangle: Sum of Interior Angles and Exterior Angle Theorem by @MathTeacherGon
Parallelogram Class 9. Find the angle. Solving intermediate question with ease. #maths #geometry
How to find the missing angles formed by intersecting lines / Finding angles between lines
How do you find the angle? Let’s see…
How To Use Reference Angles to Evaluate Trigonometric Functions
Find the Value of Angle X in this Triangle | Fast & Easy Tutorial
How to Determine the Angle Given the Value of Cosine
Finding the Missing Angle of a Triangle: A Step-by-Step Guide | Triangles | Math with Mr. J
Finding the values of vertical angles - Online Tutor - Free Math Videos
Applying the Relationship of Corresponding Angles to Find the Value of x
Exterior Angle Theorem For Triangles, Practice Problems - Geometry
Find the Value of Angle D in this Triangle | Fast & Easy Explanation
Find the value of cosine when given the angle
Missing Angles in Triangles | How to Find the Missing Angle of a Triangle Step by Step
Can You Find Angle X? | Geometry Challenge!
Trigonometry - Find the value when the angle is larger than 90 or smaller than 0
Calculate angle X in a 5-sided irregular Polygon | Learn how to Solve this Geometry problem Quickly
Комментарии
 0:05:25
0:05:25
 0:04:52
0:04:52
 0:01:09
0:01:09
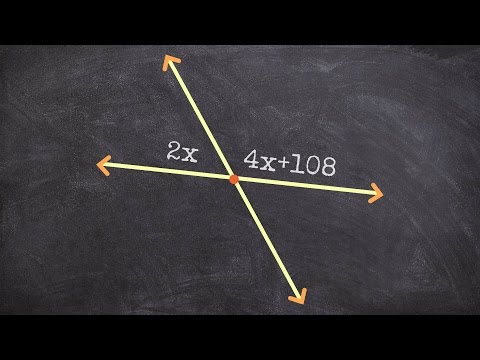 0:03:05
0:03:05
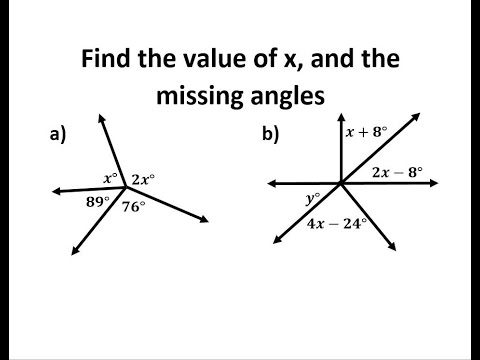 0:10:07
0:10:07
 0:04:48
0:04:48
 0:05:57
0:05:57
 0:07:00
0:07:00
 0:00:37
0:00:37
 0:02:52
0:02:52
 0:15:46
0:15:46
 0:10:59
0:10:59
 0:04:53
0:04:53
 0:00:36
0:00:36
 0:05:14
0:05:14
 0:03:11
0:03:11
 0:02:01
0:02:01
 0:12:41
0:12:41
 0:04:13
0:04:13
 0:01:55
0:01:55
 0:03:40
0:03:40
 0:08:44
0:08:44
 0:10:35
0:10:35
 0:03:17
0:03:17