filmov
tv
Arithmetic geometric mean inequality

Показать описание
In this video I give an elementary proof of the arithmetic-geometric mean inequality using calculus 1 techniques. This inequality states that the arithmetic mean of a list of positive numbers is always greater than or equal to its geometric mean.
I would like to thank Alex Zorba for providing me with the idea of the proof!
I would like to thank Alex Zorba for providing me with the idea of the proof!
A Visual Proof of the Arithmetic Geometric Mean Inequality
The arithmetic-geometric mean inequality
Arithmetic mean vs Geometric mean | inequality among means | visual proof
Inequality Proofs (Example 4 of 5: Arithmetic & Geometric Means)
Arithmetic-Geometric Mean Inequality
Prove the Inequality of Arithmetic and Geometric Means (AM-GM inequality)
Problem-Solving Trick No One Taught You: RMS-AM-GM-HM Inequality
Arithmetic geometric mean inequality
Finding the Minimum Value of 2x + y: Optimization with AM-GM Inequality
L16 | MII 2 | GM AM Inequality | Arithmetic Geometric Mean | Real Analysis | NEP | UG Maths | B Sc
Arithmetic Geometric Mean Inequality
Arithmetic Mean-Geometric Mean Visual Proof Compilation
How to Prove Arithmetic Mean Geometric Mean Inequality
AM-GM Inequality via negative space
AM-GM Inequality VI (visual proof)
AM-GM Inequality II
Proving the Arithmetic Geometric Mean inequality (Am - Gm proof) with induction
AM-GM Inequality II (visual proof)
AM-GM Inequality | Arithmetic Mean Geometric Mean Inequality
Arithmetic Mean-Root Mean Square Inequality (visual proof)
Mean Inequalities
Fold the AM-GM inequality
Arithmetic Mean-Geometric Mean Inequality
Root-Mean Square, Arithmetic Mean, Geometric Mean and Harmonic mean Inequalities.
Комментарии
 0:05:11
0:05:11
 0:10:08
0:10:08
 0:01:39
0:01:39
 0:05:25
0:05:25
 0:00:37
0:00:37
 0:06:24
0:06:24
 0:08:24
0:08:24
 0:17:18
0:17:18
 0:07:32
0:07:32
 0:07:50
0:07:50
 0:12:34
0:12:34
 0:05:01
0:05:01
 0:10:36
0:10:36
 0:01:00
0:01:00
 0:02:16
0:02:16
 0:00:55
0:00:55
 0:19:11
0:19:11
 0:01:40
0:01:40
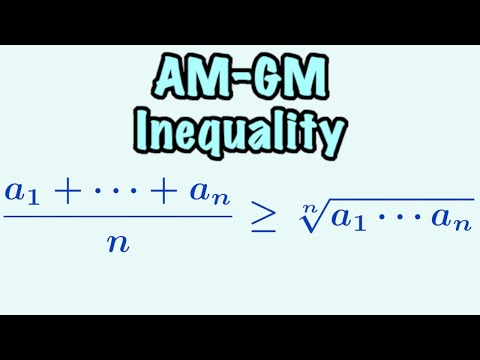 0:12:45
0:12:45
 0:02:01
0:02:01
 0:01:00
0:01:00
 0:00:54
0:00:54
 0:06:39
0:06:39
 0:00:16
0:00:16