Problem-Solving Trick No One Taught You: RMS-AM-GM-HM Inequality

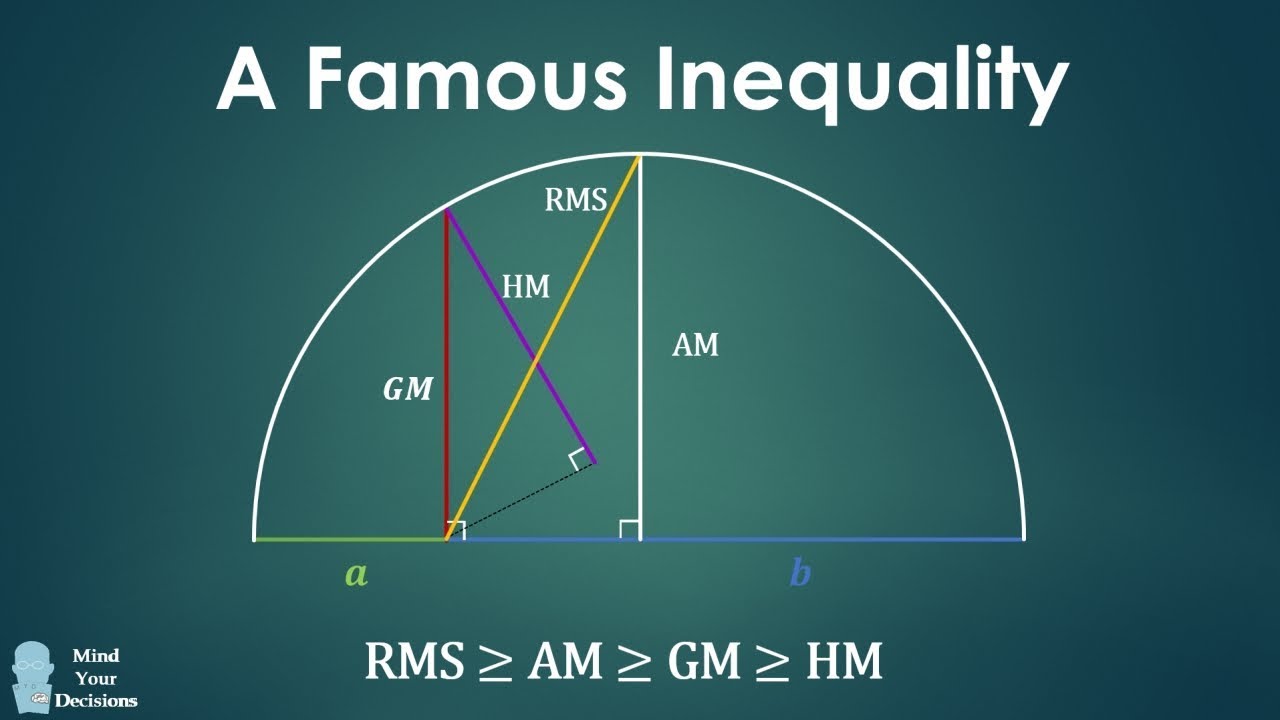
This inequality is famous in math competitions and in theoretical proofs. But why is it true? The video presents a great geometric visualization and proof for two variables. Pay attention--I'll use this inequality in an upcoming video!

Link to proofs of generalized case

Playlist to watch all videos on MindYourDecisions

This is the only channel to feature math topics suggested by people from around the world. Sadly some textbooks, websites, and other channels think math is limited to specific topics from certain countries--and they are vocal about it. Support the channel on Patreon so we can prove math really is universal:

If you buy from the links below I may receive a commission for sales. This has no effect on the price for you.

My Books
"The Joy of Game Theory" shows how you can use math to out-think your competition. (rated 4/5 stars on 34 reviews)

"The Irrationality Illusion: How To Make Smart Decisions And Overcome Bias" is a handbook that explains the many ways we are biased about decision-making and offers techniques to make smart decisions. (rated 4.6/5 stars on 3 reviews)

"Math Puzzles Volume 1" features classic brain teasers and riddles with complete solutions for problems in counting, geometry, probability, and game theory. Volume 1 is rated 4.4/5 stars on 13 reviews.

"Math Puzzles Volume 2" is a sequel book with more great problems. (rated 4.3/5 stars on 4 reviews)

"Math Puzzles Volume 3" is the third in the series. (rated 4/5 stars on 6 reviews)

"40 Paradoxes in Logic, Probability, and Game Theory" contains thought-provoking and counter-intuitive results. (rated 4.4/5 stars on 13 reviews)

"The Best Mental Math Tricks" teaches how you can look like a math genius by solving problems in your head (rated 4.8/5 stars on 5 reviews)

"Multiply Numbers By Drawing Lines" This book is a reference guide for my video that has over 1 million views on a geometric method to multiply numbers. (rated 5/5 stars on 4 reviews)

Connect with me

[Jack_Callcott_AU]

I learned this for the first time when I was about 40 yrs old. This geometric proof is just so elegant. Such a shame I never encountered it at school or university.

[billy.]

*Thank you for the math lesson.* I've gained much more knowledge by watching this than those debatable puzzles.

[morethejamesx]

Hey this is Presh Talkwalker

[usehbijkbv]

How to get root(ab): Use proportions. Let c be the length of the red segmant. Then a/c = c/b, which implies c^2 = ab, since the triangles are similar.

[GermansEagle]

Seriously, how have I never heard of this proof.

[deadfish]

It took me quite a while to work out where you got sqrt(ab) and xAM=GM^2. So you could go into those more explicitly

[koenth]

Wow, very amazing and elegant! We can even see other things from the graph, for example that AM/RMS >= HM/GM.
Explanation: These ratios are the cosines of the top angles. And the top angles are arctan((b-a)/2GM) and arctan((b-a)/2AM) respectively. Since arctan is ascending and AM and GM are in the denominator, the right top angle is smaller than the left top angle. And since cosine is a descending function on the interval [0, pi/2], the ratio AM/RMS is larger (or equal) than RM/GM.

[Trinexx]

I have algebraic proofs of the inequalities using proof by contradiction:

First, suppose that RMS<AM
((a^2+b^2)/2)^(1/2)<(a+b)/2
Now we can do some algebra and end up with
(2*(a^2+b^2))^(1/2)<a+b
Now make a substitution b = a*k
(2*(a^2+(a*k)^2))^(1/2)<a+a*k
(2*a^2*(k^2+1))^(1/2)<a*(k+1)
(2*(k^2+1))^(1/2)<k+1
Now we square both sides
2*k^2+2<k^2+2*k+1
k^2-2*k+1<0
(k-1)^2<0
Contradiction
∴RMS≥AM

Next, suppose that AM<GM
(a+b)/2<(a*b)^(1/2)
Simplify
(a+b)<2*(a*b)^(1/2)
Make the same substitution
(a+a*k)<2*(a*a*k)^(1/2)
1+k<2*k^(1/2)
Square both sides
k^2+2*k+1<4*k
k^2-2*k+1<0
(k-1)^2<0
Contradiction
∴AM≥GM

Last, suppose that GM<HM
(a*b)^(1/2)<2*a*b/(a+b)
Simplify
(a*b)^(1/2)*(a+b)<2*a*b
Again, make the substitution b = a*k
k^(1/2)*(k+1)<2*k
Square both sides
k*(k+1)^2<4*k^2
k^3+2*k^2+k<4*k^2
k^2+2*k+1<4*k
k^2-2*k+1<0
(k-1)^2<0
Contradiction
∴GM≥HM

I don't think these arguments apply if any of the numbers are negative or complex, and I'm not sure how to generalize to more numbers than 2. With that said, I think it's really amusing that all 3 hinge on the same inequality of (k-1)^2<0

Here is a bonus proof of GM≥HM, given that we already know that AM≥GM
GM<HM
HM=GM^2/AM
GM<GM^2/AM
1<GM/AM
AM<GM
Contradiction
∴GM≥HM

[titan]

IMO, this is seriously one of your best videos ever. This one gets to show us that Geometry, I believe, is intrinsically linked to all of Mathematics, even with the most seemingly unrelated topic. What a beautiful proof, Presh. Thank you!

[Epoch]

A video on why each of these means is useful would be nice. I'm not a mathematician and sure I can go look it up myself, but it would be much easier for me if you did it. Jokes aside, an in depth explanation of these various means would make a video I would definitely watch.

[looney]

This is the best video you've made thus far. A cool visualization / geometric proof of a useful theorem. Nice job

[ankitjain]

Me a 36 years old failure in both professional and personal life loves your video try to solve questions, watch them many times. They are lifeline for me.

[ffggddss]

+ Presh: At 3m50s: You can also quickly verify that this altitude is the GM by similar triangles, because a/h = h/b
And I really like your geometric demo of that chain of inequalities!!

BTW, you might mention that all these means are related by being "functional transforms" of the simple (arithmetic) mean. A "transformed mean, " TM, using a monotonic function f, is:

TM( ֿx ) = f⁻¹(AM(f( ֿx )))
where ֿx = x[1...n]; AM(f( ֿx )) = (1/n)∑ᵢ₌₁ⁿ f( xᵢ )

So:
• when f(x) = x², f⁻¹(x) = √x, and TM = RMS
• when f(x) = x, f⁻¹(x) = x, and TM = AM
• when f(x) = ln(x), f⁻¹(x) = eˣ, and TM = GM
• when f(x) = 1/x, f⁻¹(x) = 1/x, and TM = HM

Neat, huh? ;–)

PS: I suspect that some property of each function – maybe something involving the second derivative – can be used to arrive at those inequalities, but I haven't delved into that.
Actually, looking at the list, I'm getting a very strong hunch . . .

Fred

[ahmedbaig]

I should be similar with all these series. Arithmetic Means is used in Statistics. Geometric means is used in calculation of population and compound interest. Wonderfully you have proveded some associations with other two.

[andabata]

Frank K.
There is also a rather beautiful generalization: Let t be any real number, and for any POSITIVE x1, x2, ..., xn, define M[t](x1, x2, ..., xn) = (Sum[(xk)^t, {k, 1, n}])^(1/t). Then if t1 < t2, we have M[t1] ≤ M[t2], with equality iff all xk are equal. In particular, M[-1] = HM, M[0] = GM, M[1] = AM and M[2] = RMS, giving the result in the video. It is also interesting to note that Limit(t -> -Inf) M[t] = min{x1, x2, ..., xn} and Limit(t -> +Inf) M[t] = max{x1, x2, ..., xn}.

[shanmugasundaram]

The video description of all the means merging together when a=b is wonderful.

[raghavagarwal]

Really helpful. Thank you very much. I am a twelth grader and have never seen such an interesting proof of this inequality.

[MyOneFiftiethOfADollar]

You, indisputably have the best technical/math presentation platform on the web. I would be filthy rich if I had a buck for every comment you have received begging you to disclose how you pulled this off?

The animation and capacity to explain and erase stuff clearly is world class.

[ashleypkumlvu]

Thank you, I always poor in math, but your lesson truly raises me up. I am in a tremendous excitment of handle some of these difficulties. Thanks again!💕💕💕

[PhilipBlignaut]

The best description regarding means ever!