filmov
tv
Limit of sqrt(9x^6 - x)/(x^3 + 1) as x approaches infinity
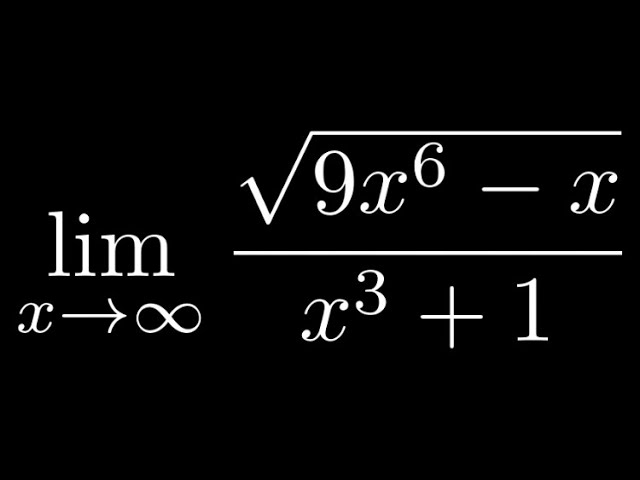
Показать описание
Limit of sqrt(9x^6 - x)/(x^3 + 1) as x approaches infinity. We divide the numerator and denominator by the sqruare root of x^6 to do this. Note sqrt(x^6) = x^3 in this problem because x is approaching infinity.
If you enjoyed this video please consider liking, sharing, and subscribing.
There are several ways that you can help support my channel:)
************Udemy Courses(Please Use These Links If You Sign Up!)*************
Abstract Algebra Course
Advanced Calculus Course
Calculus 1 Course
Calculus 2 Course
Calculus 3 Course
Calculus 1 Lectures with Assignments and a Final Exam
Calculus Integration Insanity
Differential Equations Course
Differential Equations Lectures Course (Includes Assignments + Final Exam)
College Algebra Course
How to Write Proofs with Sets Course
How to Write Proofs with Functions Course
Trigonometry 1 Course
Trigonometry 2 Course
Statistics with StatCrunch Course
Math Graduate Programs, Applying, Advice, Motivation
Daily Devotionals for Motivation with The Math Sorcerer
Thank you:)
If you enjoyed this video please consider liking, sharing, and subscribing.
There are several ways that you can help support my channel:)
************Udemy Courses(Please Use These Links If You Sign Up!)*************
Abstract Algebra Course
Advanced Calculus Course
Calculus 1 Course
Calculus 2 Course
Calculus 3 Course
Calculus 1 Lectures with Assignments and a Final Exam
Calculus Integration Insanity
Differential Equations Course
Differential Equations Lectures Course (Includes Assignments + Final Exam)
College Algebra Course
How to Write Proofs with Sets Course
How to Write Proofs with Functions Course
Trigonometry 1 Course
Trigonometry 2 Course
Statistics with StatCrunch Course
Math Graduate Programs, Applying, Advice, Motivation
Daily Devotionals for Motivation with The Math Sorcerer
Thank you:)
Limit of sqrt(9x^6 - x)/(x^3 + 1) as x approaches infinity
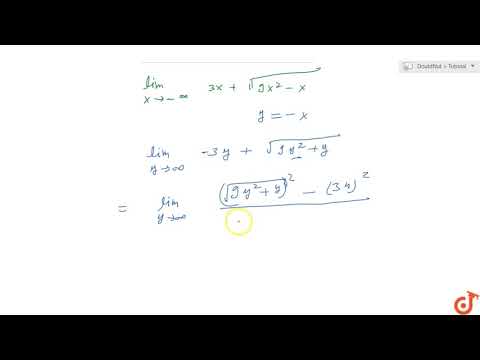
Limit of sqrt(9x^2 + 3x) - 3x as x approaches infinity
Limit of (sqrt(x) - 3)/(x - 9) as x approaches 9
Evaluating Limits at Infinity of Rational Functions with Square Roots (Example)
When mathematicians get bored (ep1)
Evaluate the limit at infinity with square root
Limit of (5x + 6)/(9x - 4) as x approaches infinity
Evaluate lim x-›3 (√(x+6)-3)/(x-3)
Find the limit as x approaches infinity of (sqrt(x^2 + 2x +3) -x).
Learn how to evaluate a limit at infinity
lim as x approaches 3, (x^2 - 9)/(x-3)
Find limit x approaches 9: (9-x)/(3-square root x)
How to Find the Limit of the Square Root of x as x approaches Infinity #shorts
Find limit at Infinity | sqrt(1+4x^6)/(2-x^3) x approaches infinity | general solution
Evaluate a limit at infinity with a radical in denominator
Limit of (7x^2 + x)/(4x^3 + 9x^2 + x) as x approaches infinity
Memorization Trick for Graphing Functions Part 1 | Algebra Math Hack #shorts #math #school
Limits at Infinity & Horizontal Asymptotes
Test Limit as x approaches minus infinity for Square root Rationalization
Limit as x goes to negative infinity AGAIN!
Tamasha Dekho 😂 IITian Rocks Relatives Shock 😂😂😂 #JEEShorts #JEE #Shorts
Find the Limit of sqrt(x) as x Approaches Infinity
Write the value of `(lim)_(x-mt-oo)(3x+sqrt(9x^2-x))`
Find the limit as x approaches infinity for (5x^3+2x)/(2x^3-4x^2+ 5x)
Комментарии
 0:03:42
0:03:42
 0:04:36
0:04:36
 0:01:52
0:01:52
 0:04:53
0:04:53
 0:00:37
0:00:37
 0:01:37
0:01:37
 0:00:48
0:00:48
 0:02:54
0:02:54
 0:04:46
0:04:46
 0:01:40
0:01:40
 0:00:33
0:00:33
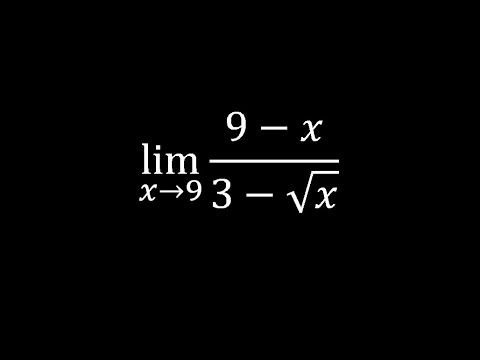 0:07:08
0:07:08
 0:00:23
0:00:23
 0:08:25
0:08:25
 0:03:14
0:03:14
 0:00:46
0:00:46
 0:00:15
0:00:15
 0:19:24
0:19:24
 0:05:50
0:05:50
 0:08:09
0:08:09
 0:00:13
0:00:13
 0:01:13
0:01:13
 0:02:45
0:02:45
 0:02:13
0:02:13