Discrete Math 2 - Tutorial 17 - More Techniques

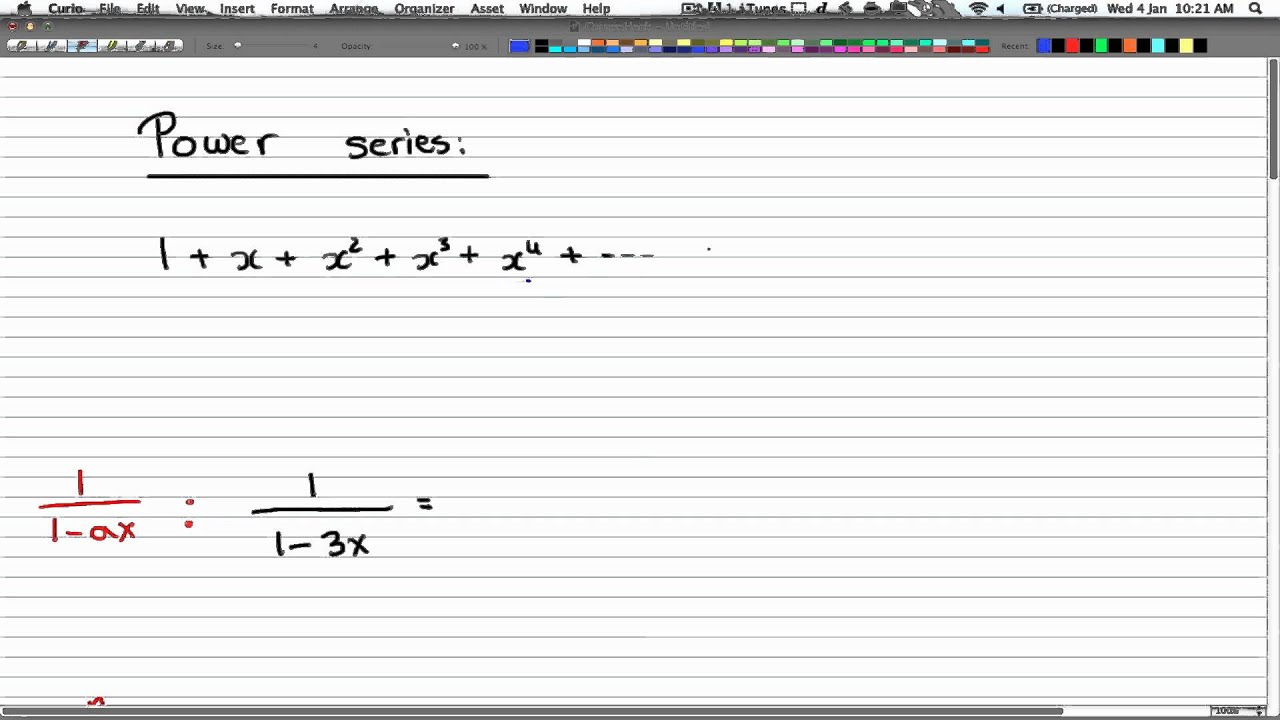
Generating Functions.
This is a foundation for finding coefficients.
This is a summary of some of the cases you could see.

Please comment, rate and subscribe.

[coursehack]

1/(1-x) = (1-x) to the power of (-1); this is a form of the binomial theorem. If you use the binomial expansion, you'll get the summation form.

Try to memorize the forms, that way you'll always be able to identify them later on...
cuz you'll be expected to know these terms throughout the course.

[coursehack]

think about this way... if 1/(1-x^2) gives you 1+x^2+x^4+x^6+..., wat ur looking for is exactly the same but with everything multiplied by x... so, if u multiply x you get... x/(1-x^2) = x+x^3+x^5+x7+..., now all ur missing is the 1 in the beginning, so just add it to both sides and you'll end up with 1+(x/(1-x^2)) = 1+x+x^3+x^5+x^7+...

[garfieldnate]

This was a little confusing because the factorial is not defined for negative integers. I find that n choose r makes more sense when using the falling power version, and falling powers are defined for negative numbers.

[vivvpprof]

Is there such a thing as negative factorial? Like (-n)! ??