filmov
tv
Mathematical integration without calculus

Показать описание
I show how to convert an area measurement problem into a mass measurement problem that is easier to solve. In general, this idea of converting measurement problems into different spaces is very powerful, and may prove useful in the future.
Mathematical integration without calculus
Math Integration Timelapse | Real-life Application of Calculus #math #maths #justicethetutor
Integration (Calculus)
Dear calculus students, stop using u sub
when calculus students use trig identities too early
Calculus in a nutshell
Seven Math Books for Seven Math Subjects You can Learn Without Calculus
Everyone was so quite for this integral
Integration Tutorials! #mathwithprofessorv #integralcalculus #trigsubstitution #calculusvideos
Tutorials & Lectures for Calculus 1, 2, and 3! #mathwithprofessorv #calculusvideos #integrals
Numerical Integration is nice! #math #fy #short #calculus #mathematics #integration
Understand Calculus in 1 minute
Integration Tricks (That Teachers Won't Tell You) for Integral Calculus
Integration and the fundamental theorem of calculus | Chapter 8, Essence of calculus
Calculus - How to find the bounds of a triple integral
Calculus - Definite Integrals
Summing integers using calculus!
Basic Integration Problems
What is Integration? Finding the Area Under a Curve
Introduction to integral calculus | Accumulation and Riemann sums | AP Calculus AB | Khan Academy
Calculus 1 - Integration & Antiderivatives
Legendary Calculus Book for Self-Study
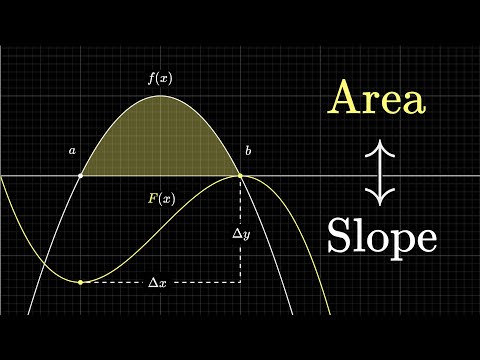
What does area have to do with slope? | Chapter 9, Essence of calculus
Finding the Area Between Two Curves by Integration
Комментарии
 0:05:46
0:05:46
 0:00:09
0:00:09
 0:07:04
0:07:04
 0:08:40
0:08:40
 0:00:43
0:00:43
 0:03:01
0:03:01
 0:12:47
0:12:47
 0:00:29
0:00:29
 0:00:36
0:00:36
 0:00:54
0:00:54
 0:00:10
0:00:10
 0:00:57
0:00:57
 0:11:26
0:11:26
 0:20:46
0:20:46
 0:04:56
0:04:56
 0:07:15
0:07:15
 0:01:00
0:01:00
 0:14:13
0:14:13
 0:08:18
0:08:18
 0:04:52
0:04:52
 0:40:04
0:40:04
 0:00:23
0:00:23
 0:12:39
0:12:39
 0:07:52
0:07:52