filmov
tv
Prove that for every 𝒏∈ℕ, 𝟑^𝟔𝒏−𝟐^𝟔𝒏 is divisible by 35 | Moscow Mathematical Olympiad Problem

Показать описание
We apply a special formula to complete the proof that for every positive integer n, 3^6n - 2^6n is divisible by 35.
Inequality Mathematical Induction Proof: 2^n greater than n^2
Example of Proof by Induction 3: n! less than n^n
Induction Inequality Proof Example 4: n! greater than n²
#20 prove induction n^3- n is divisible by 3 mathgotserved mathematical precalculus discrete princ
Prove by induction, Sum of the first n cubes, 1^3+2^3+3^3+...+n^3
Induction Inequality Proof: 3^n is greater than or equal to 2n + 1
Induction Inequality Proof Example 5: 2^n ≥ n²
Induction Inequality Proof Example 3: 5^n + 9 less than 6^n
Induction: Divisibility Proof example 6 (a^n - b^n is divisible by a - b)
Sum of n squares | explained visually |
Mathematical Induction - Proof of ∑r=n(n+1)/2 | ExamSolutions
Induction Inequality Proof Example 1: Σ(k = 1 to n) 1/k² ≤ 2 - 1/n
What does a ≡ b (mod n) mean? Basic Modular Arithmetic, Congruence
Proof: Supremum of {n/(n+1)} = 1 | Real Analysis
Prove limit (x^n - a^n)/(x - n) = nx^(n - 1) as x approaches a
The Hierarchy of Big Functions || n^n greater than n! greater than e^n greater than n^100
ThanThani'n Mami Product Chhiatzia a rawn Proof ta😱😱😱🤣🤣🤣
The Legendary n^2+n+41 sequence
Proof that the Sequence (-1)^n Diverges using the Definition
Find the sum of first n squares, difference equation approach, (ft. Max!)
1.8.1 Asymptotic Notations Big Oh - Omega - Theta #1
They gave us a 1 ⭐️ review over this…
Derivation | Formula | Sum of first n squares or square numbers 1^2 + 2^2 + 3^2 + 4^2 +...n^2
SPECIAL. LATEST 2025 NIGERIA MOVIE | EGO NWOSU, CLINTON JOSHUA, KOFI ADJORLOLO, PRINCESS MAUREEEN,
Комментарии
 0:09:20
0:09:20
 0:06:14
0:06:14
 0:10:32
0:10:32
 0:15:56
0:15:56
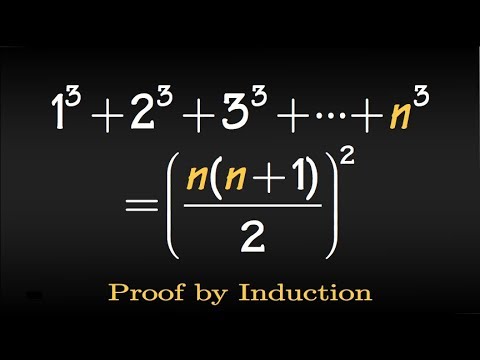 0:09:03
0:09:03
 0:08:49
0:08:49
 0:16:15
0:16:15
 0:10:42
0:10:42
 0:05:52
0:05:52
 0:02:14
0:02:14
 0:08:13
0:08:13
 0:13:09
0:13:09
 0:05:45
0:05:45
 0:10:20
0:10:20
 0:10:14
0:10:14
 0:15:49
0:15:49
 0:19:33
0:19:33
 0:07:10
0:07:10
 0:04:27
0:04:27
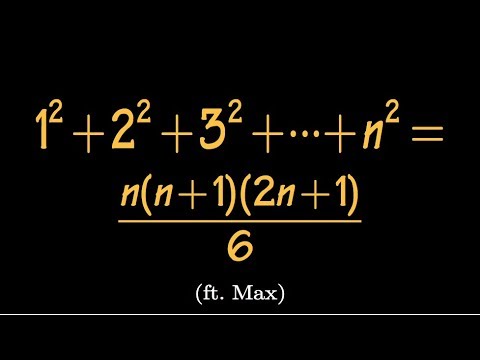 0:11:19
0:11:19
 0:15:46
0:15:46
 0:00:47
0:00:47
 0:05:30
0:05:30
 1:50:13
1:50:13