filmov
tv
#20 prove induction n^3- n is divisible by 3 mathgotserved mathematical precalculus discrete princ

Показать описание
Prove
Math Tutorials Links
Algebra
Foundations
Equations
Inequalities
Solve Systems of Equations by Graphing
TESTS
Math Tutorials Links
Algebra
Foundations
Equations
Inequalities
Solve Systems of Equations by Graphing
TESTS
#20 prove induction n^3- n is divisible by 3 mathgotserved mathematical precalculus discrete princ
Proof that n^3 - n is divisible by 3 using Mathematical Induction
Using Mathematical Induction to Prove 2^(3n) - 3^n is divisible by 5
Induction - Showing that 3^n is less than n!
Mathematical Induction Practice Problems
Induction Divisibility
Prove that n^3 + 2n is divisible by 3 using Mathematical Induction
Mathematical Induction | Show that (n³+2n) is divisible by 3
HSN | KitchenHQ featuring Chef Shahir 5th Anniversary 10.04.2024 - 02 AM
Prove by induction, Sum of the first n cubes, 1^3+2^3+3^3+...+n^3
Prove that n^3 +2n is divisible by 3 for all positive integers. Principle of Mathematical Induction
Induction: Divisibility Proof example 1 (n³ + 3n² + 2n is divisible by 6)
Prove by mathematical induction that n cubed + 2n is a multiple of 3 (n^3 + 2n)
Learn how to use mathematical induction to prove a formula
Induction Inequality Proof: 2^n greater than n^3
Prove that 11^n - 4^n is divisible by 7 for any natural number, n. [Mathematical Induction]
Inequality Mathematical Induction Proof: 2^n greater than n^2
Proof by Mathematical Induction - How to do a Mathematical Induction Proof ( Example 2 )
For any integer n prove that n^3-n is divisible by 6
Prove by the principle of mathematical induction that `(n^5)/5+(n^3)/3+(7n)/(15)` is a natural n...
Proof: a³ - a is always divisible by 6 (1 of 2: Two different approaches)
Prove that 3^n-1 is divisible by 2 for all positive integers. Mathematical Induction
Mathematical Induction - Divisibility Tests (1) | ExamSolutions
How to use Principle of Mathematical induction to prove 3+6+9...+3n=3n(n+1)/2
Комментарии
 0:15:56
0:15:56
 0:04:38
0:04:38
 0:06:17
0:06:17
 0:10:22
0:10:22
 0:18:08
0:18:08
 0:20:35
0:20:35
 0:12:23
0:12:23
 0:06:18
0:06:18
 1:00:00
1:00:00
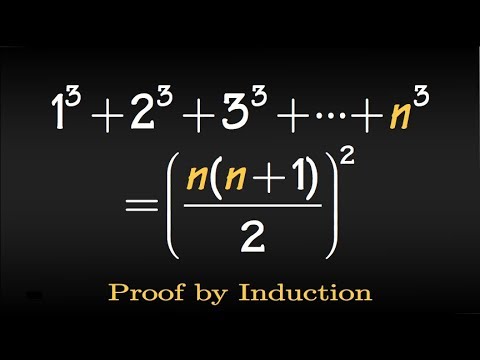 0:09:03
0:09:03
 0:03:17
0:03:17
 0:09:54
0:09:54
 0:05:45
0:05:45
 0:07:08
0:07:08
 0:10:27
0:10:27
 0:10:50
0:10:50
 0:09:20
0:09:20
 0:10:08
0:10:08
 0:04:37
0:04:37
 0:04:42
0:04:42
 0:10:15
0:10:15
 0:03:53
0:03:53
 0:08:35
0:08:35
 0:20:45
0:20:45