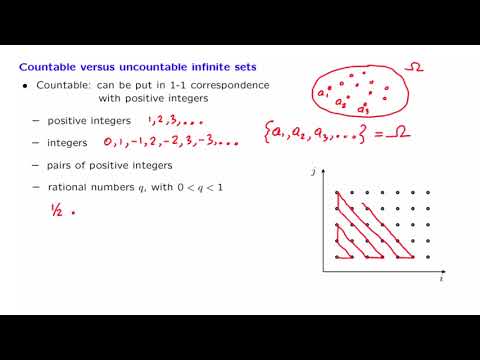
Countable: Set of finite subsets of a countable A, Set of circles with rational center and radius,..

- Let A be a countable set. Let C be the collection of all finite subsets of A. Prove that C is countable.
- Let A be the set of all circles in the plane R^2 with center (x, y) in Q^2 and radius r in Q. Show that A is countable.
- Let A be a subset of R. For any real number x, there is a positive number d such that the intersection of (x-d, x+d) and A contains at most countable points. Show that A is countable.