Collection of Finite Subsets is Countable

preview_player
Показать описание
We prove that the set consisting of finite subsets of a countable set is countable. This is a useful fact in math competitions such as the Putnam math competition.

  1. Dr. Ebrahimian
  2. Math
  3. maths
  4. Set Theory
  5. Countable
  6. Uncountable
Рекомендации по теме
Collection of Finite 0:06:41

Collection of Finite Subsets is Countable

Unveiling the Countability 0:11:38

Unveiling the Countability of Finite Subsets of Natural Numbers

Counting the finite 0:11:26

Counting the finite subsets of the naturals

Number of subsets 0:02:42

Number of subsets of a finite set

Binary Tree vs 0:22:55

Binary Tree vs All Finite Subsets of N

Problem 6. Finite 0:12:51

Problem 6. Finite subsets are varieties

Counting subsets of 0:03:52

Counting subsets of a finite set

Finite Sets and 0:01:59

Finite Sets and Infinite Sets | Don't Memorise

How to count 0:11:52

How to count the subsets of a finite set.

Cardinality of Finite 0:09:57

Cardinality of Finite Sets

The Number of 0:04:58

The Number of Subsets of a Finite Set Binomial Theorem Proof

Finite and Infinite 0:13:21

Finite and Infinite Sets

FINITE PRODUCT OF 0:18:27

FINITE PRODUCT OF COUNTABLE SET, COLLECTION OF FINITE AND INFINITE SUBSETS OF NATURAL NUMBER

Countable: Set of 0:03:19

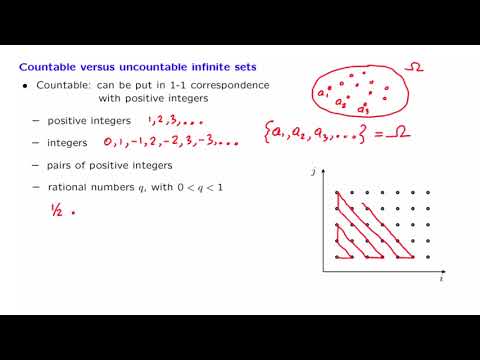
Countable: Set of finite subsets of a countable A, Set of circles with rational center and radius,..

Finite and Infinite 0:03:57

Finite and Infinite Sets

Cardinality of Infinite 0:12:32

Cardinality of Infinite Sets

What is the 0:17:15

What is the opposite of a set?

Countable and Uncountable 0:10:02

Countable and Uncountable Sets - Discrete Mathematics

Section 5.1(c), part 0:07:41

Section 5.1(c), part 4 Cardinality of subsets of finite sets

S01.8 Countable and 0:06:19

S01.8 Countable and Uncountable Sets

Counting Subsets of 0:01:00

Counting Subsets of a Finite Set and Power Sets. (Intro To Math Structures Ex1.2.2)

How many Subsets 0:00:27

How many Subsets #Finite #Math

Labtube-(Finite Math)- Number 0:15:37

Labtube-(Finite Math)- Number of subsets of a finite set

Algebra II 15.4d, 0:03:36

Algebra II 15.4d, Subsets of a finite set

Комментарии
Автор

Much better than the other proofs of this I've seen. Way more intuitive and uses easily provable results

yajaman
Автор

You just saved me from getting an F on my real analysis final Dr. Ebrahimi! Much appreciated!

parsashirani
Автор

I like it. Here is a sketch of another way. Our base countable set is isomorphic to the Natural numbers. Define a map that takes any finite subset of natural numbers to the the product of all the primes indexed by elements of the subset, e.g. {1, 3} maps to 2*5=10. {1} maps to the empty set.

petersiracusa
Автор

hey i have a doubt! in 4:24, while writing the expression for Sn+1 in terms of union, we have A belongs to Sn right? but Sn also has many other elements, so what about their union with {Xk} ?

novideos...