Two Countable Sets

Показать описание

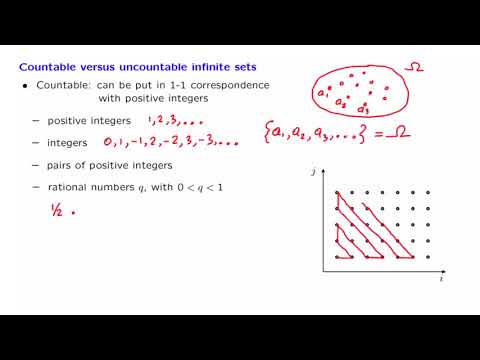
This is a short animation with two animations showing that the set of integers is a countable set (in bijection with the set of Natural numbers) and that the set of ordered pairs of integers is also a countable set.

Here is a related video proving that function composition is associative:

#shorts #visualproof #mathshorts #mathvideo #math #bijection #mtbos #manim #animation #theorem #pww #proofwithoutwords #visualproof #proof #iteachmath #function #injection #surjectivefunction #injectivefunction #surjective #injective #naturalnumbers #integers #countableset #infinity

To learn more about animating with manim, check out:

Рекомендации по теме

Комментарии

Visual proofs are some of the most elegant things in the universe. These need to be mandatory in teaching math. If I had been introduced to these concepts in this way, I would've learned to love math much earlier.

erinmcdonald

It would be interesting to see a bijective map from N to the set of Algebraic Numbers I think.

amukh_dev

"Can you find a formula..."

No, sir. I cannot. But your videos are entertaining, so I am binging your shorts before I go to sleep.

inskeeprulerable

F(x, y)=
X=x+1 Y=y if x, y are even
X=x Y=y+1 if x odd y even
X=-x Y=y if x, y odd
X=x Y=-y if x even y odd

bogdangiusca

the Z x Z mapping is similar to proving that the set of gaussian integers (complex numbers where the real and imaginary part are integers) is countable. Very nice.

Ninja

Back in my college days, when there was no Manim, we used to draw in turtle to visualize that.

import turtle
import time

def draw_points(n):
turtle.speed(0)

points = [(0, 0)]
x, y = 0, 0
directions = [(0, 1), (1, 0), (0, -1), (-1, 0)]
direction_index = 0
steps = 1
step_count = 0

while len(points) < n:
dx, dy = directions[direction_index]
x += dx
y += dy
points.append((x, y))
step_count += 1

if step_count == steps:
step_count = 0
if direction_index == 1 or direction_index == 3:
steps += 1
direction_index = (direction_index + 1) % 4

for point in points:
x, y = point
turtle.goto(x * 20, y * 20)
turtle.dot(5)
print(f"({x}, {y})")
time.sleep(0.1)

turtle.done()

n = int(input("Number of Iteration: "))
draw_points(n)

yoursamlan

This will form a Arithmetic progression or AP

VIPPerson

Define f: N×N -> N
f(m, n)=2^m•2^n is an injection.

Define g: N -> N×N
g(n)=(n, n-1) is also an injection.

By Shröder-Bernstein theorem, there must be a bijection from N to N×N.◼️

This also shows that the set of rational numbers is countable (how?).

Edit: As corrected by MathVisualProofs... f(m, n) is not one-one. Because f(1, 4)=f(2, 3) and there are many such examples. So take:
f(m, n)=2^m•3^n which is indeed one-one.
Also take:
g(n)=(n, n+1).
(n, n-1) doesn't make sense because n-1 doesn't not belong to N for n = least element of N.

solitary