filmov
tv
Proof Of The Basel Problem

Показать описание
First conceived by Pietro Mengoli in 1650, Leonhard Euler proved this seemingly impossibly infinite series in 1734. The problem is named after Basel, the town in which Euler was born.
Why is pi here? And why is it squared? A geometric answer to the Basel problem
Cauchy's Proof of the Basel Problem | Pi Squared Over Six (3blue1brown SoME1 Entry)
Euler's Original Proof Of Basel Problem: Σ(1/n²)=π²/6 — BEST Explanation
The Basel Problem Part 2: Euler's Proof and the Riemann Hypothesis
The Basel Problem and Euler's proof
But HOW did Euler do it?! A BEAUTIFUL Solution to the FAMOUS Basel Problem!
If I did this in 1734 I'd be World Famous
Proof Of The Basel Problem
What's this infinite sum?
An easy solution to the Basel problem
a spectacular solution to the Basel problem (sum of 1/n^2 via a complex integral)
The Basel Problem Part 1: Euler-Maclaurin Approximation
Why greatest Mathematicians are not trying to prove Riemann Hypothesis? || #short #terencetao #maths
Proof by intuition done by Leonhard Euler, sum of 1/n^2, (feat. Max)
Amazing Proof of Basel Problem | How value of Pi is Estimated | Prashant Jain
The Simplest Proof Of The Basel Problem [Difficulty: 2]
This Basel Problem Integral Blew My Mind...
Basel Problem #shorts
Basel Problem
Solving the Basel problem via fluid dynamics
Euler's brilliant solution to the Basel problem vs Cauchy's cool residue theorem approach
Why Is PI There?? - The Basel Problem | Laid Back Math, Episode 24
Apostol's Solution to the Basel Problem
Three Levels of Math Understanding, With Math Example: Proving the Basel Problem
Комментарии
 0:17:08
0:17:08
 0:09:59
0:09:59
 0:13:59
0:13:59
 0:58:32
0:58:32
 0:07:38
0:07:38
 0:18:05
0:18:05
 0:03:57
0:03:57
 0:12:41
0:12:41
 0:00:31
0:00:31
 0:17:52
0:17:52
 0:22:27
0:22:27
 0:59:07
0:59:07
 0:00:38
0:00:38
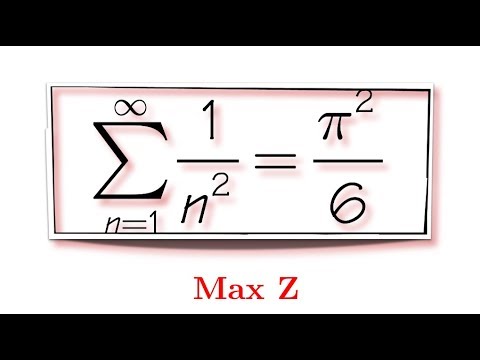 0:14:13
0:14:13
 0:07:40
0:07:40
 0:11:35
0:11:35
 0:01:00
0:01:00
 0:00:44
0:00:44
 0:01:26
0:01:26
 0:01:00
0:01:00
 0:11:56
0:11:56
 0:12:33
0:12:33
 0:13:37
0:13:37
 0:10:16
0:10:16