filmov
tv
The Basel Problem Part 1: Euler-Maclaurin Approximation
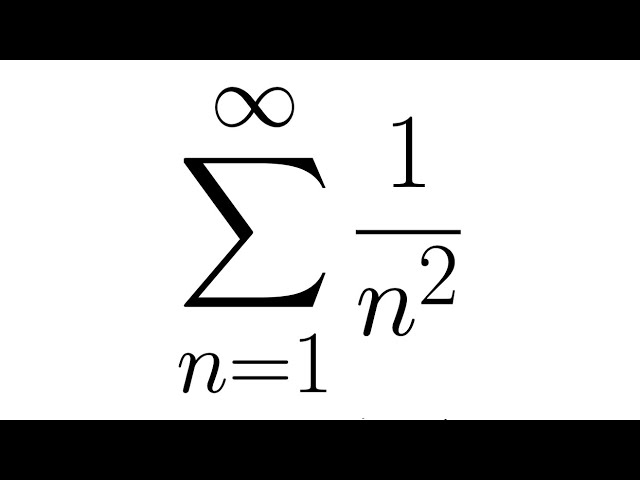
Показать описание
This is the first video in a two part series explaining how Euler discovered that the sum of the reciprocals of the square numbers is π^2/6, leading him to define the zeta function, and how Riemann discovered the surprising connection between the zeroes of the zeta function and the distribution of the primes, leading ultimately to his statement of the Riemann Hypothesis. This video focuses on how Euler developed a method to approximate this sum to 17 decimal places, as well as how the Bernoulli numbers naturally appear as part of this problem.
Theme music by Keith Welker.
Theme music by Keith Welker.
The Basel Problem Part 1: Euler-Maclaurin Approximation
Solving the Basel Problem using the Fourier Series (Part 1)
The Basel Problem, Pt.1
The Basel Problem, Part 1.
Why is pi here? And why is it squared? A geometric answer to the Basel problem
The Basel Problem (1 of 9: Prologue)
The Basel Problem Part 2: Euler's Proof and the Riemann Hypothesis
Cauchy's Proof of the Basel Problem | Pi Squared Over Six (3blue1brown SoME1 Entry)
But HOW did Euler do it?! A BEAUTIFUL Solution to the FAMOUS Basel Problem!
The Basel Problem
If I did this in 1734 I'd be World Famous
Euler's Original Proof Of Basel Problem: Σ(1/n²)=π²/6 — BEST Explanation
a spectacular solution to the Basel problem (sum of 1/n^2 via a complex integral)
Solving the Basel problem via fluid dynamics
The Basel Problem and Euler's proof
Incredible Proof for the BASEL PROBLEM by Greek-American mathematician Tom Apostol
Part 1. Leonhard Euler's solution to the BASEL PROBLEM.
CalcBLUE 3 : Ch. 16.4 : Example - The Basel Problem 1
The Basel Problem Proof
Solve the Basel problem - the traditional way
Using High School Mathematics(Kinda) to Solve the Basel Problem (Part 1) - A Level H2 Maths 9758
Complex Analysis: The Basel Problem
Proof Of The Basel Problem
33.1 The Basel problem
Комментарии
 0:59:07
0:59:07
 0:14:01
0:14:01
 0:20:41
0:20:41
 0:32:45
0:32:45
 0:17:08
0:17:08
 0:08:41
0:08:41
 0:58:32
0:58:32
 0:09:59
0:09:59
 0:18:05
0:18:05
 0:10:47
0:10:47
 0:03:57
0:03:57
 0:13:59
0:13:59
 0:22:27
0:22:27
 0:01:00
0:01:00
 0:07:38
0:07:38
 0:12:50
0:12:50
 0:37:48
0:37:48
 0:04:59
0:04:59
 0:02:15
0:02:15
 0:01:23
0:01:23
 0:11:36
0:11:36
 1:14:53
1:14:53
 0:12:41
0:12:41
 0:12:34
0:12:34