filmov
tv
Proof by intuition done by Leonhard Euler, sum of 1/n^2, (feat. Max)
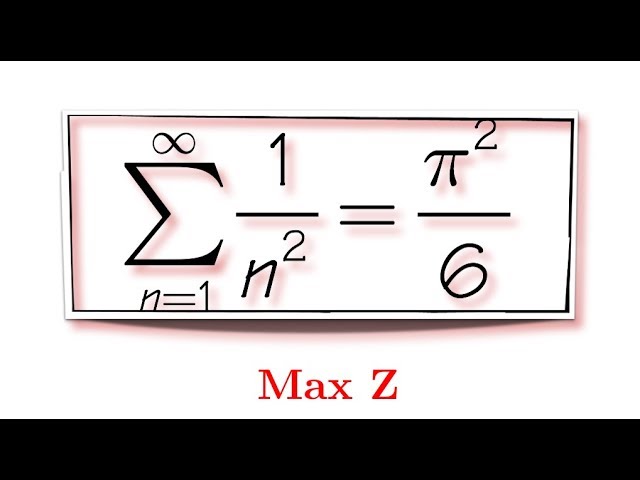
Показать описание
Sum of 1/n^2,
pi^2/6,
blackpenredpen,
math for fun,
Proof by intuition done by Leonhard Euler, sum of 1/n^2, (feat. Max)
Math and Intuition
The Intuition Behind Proof by Induction
Intuition for Separable Differential Equations #SoME2
Can You Trust Your Intuition?
Proof and Intuition for the Weierstrass Approximation Theorem
A Proof of Childish Intuition
3 ways your intuition is telling someone is lying to you.
SUPER EASY Techniques to Unlock Your #intuition
Dramatically Improve Your Intuition By Using This 1 Trick… | Dom The Hypnotist
The science behind intuition
Seeing Through Someones BS #Intuition #Perception #Relationships
Never ignore your intuition. #dating #datingadvice #marriage #relationship #relationships
How Game Theory Beats Intuition
Use Your Intuition When Accepting Advice - David Shands & Donni Wiggins - Social Proof Podcast 4...
Women’s Intuition is overrated? #relationships #dating #marriage #shorts
How to Understand Math Intuitively?
Intuition, Proof, and Certainty (GROUP 2)
Intuition, Paradoxes, and Proof: THE MAN WHO KNEW INFINITY
How To Follow Your Intuition Without Emotion
Cauchy integral theorem intuition and proof
You NEED to trust your intuition because this.. 😳💫 | #shorts #intuition
How to eat intuitively… #thebodyknows #intuition #innerguidance #innerwisdom #trustself #carnivore...
What is Intuition?
Комментарии
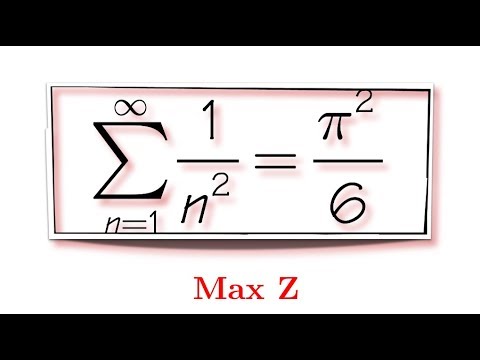 0:14:13
0:14:13
 0:00:58
0:00:58
 0:22:10
0:22:10
 0:05:21
0:05:21
 0:00:31
0:00:31
 0:28:53
0:28:53
 0:02:34
0:02:34
 0:00:34
0:00:34
 0:53:10
0:53:10
 0:00:20
0:00:20
 0:00:56
0:00:56
 0:00:34
0:00:34
 0:00:24
0:00:24
 0:00:54
0:00:54
 0:00:44
0:00:44
 0:00:15
0:00:15
 0:08:28
0:08:28
 0:05:04
0:05:04
 0:30:57
0:30:57
 0:00:37
0:00:37
 0:08:41
0:08:41
 0:00:50
0:00:50
 0:00:17
0:00:17
 0:00:53
0:00:53