filmov
tv
A Quick and Easy Diophantine Equation | Primes

Показать описание
🤩 Hello everyone, I'm very excited to bring you a new channel (SyberMath Shorts).
Enjoy...and thank you for your support!!! 🧡🥰🎉🥳🧡
If you need to post a picture of your solution or idea:
#numbertheory #diophantineequations
via @YouTube @Apple @Desmos @NotabilityApp @googledocs @canva
PLAYLISTS 🎵 :
Enjoy...and thank you for your support!!! 🧡🥰🎉🥳🧡
If you need to post a picture of your solution or idea:
#numbertheory #diophantineequations
via @YouTube @Apple @Desmos @NotabilityApp @googledocs @canva
PLAYLISTS 🎵 :
A Quick and Easy Diophantine Equation
A Quick and Easy Linear Diophantine System
A Quick and Easy Diophantine Equation | Primes
A Quick and Easy Diophantine Equation
A Quick and Easy Solution to Diophantine Exponential Equation
A Quick and Easy Diophantine System
I Solved A Quick And Easy Diophantine Equation
A Diophantine Equation with Three Variables
Mastering Diophantine Equations: Easy Methods for Finding Integer Solutions with Examples
A Quick & Easy Diophantine Equation from the SASMO
One fairly easy diophantine equation anyone can solve | mathematica
A Diophantine Equation with Integer Solutions
Solve Diophantine Equations by Factoring
A Basic Diophantine Equation!
Diophantine Equations with 1 Variable ← Number Theory ← Socratica
A simple Diophantine Equation
Simple Diophantine equation
A Great Book on Diophantine Equations
When mathematicians get bored (ep1)
A Nice Diophantine Equation in Number Theory | You Should Learn This Theorem | Math Olympiad
Simple Diophantine Equation
A Diophantine Equation | x^y=y^x
Watch this simple Diophantine Equation below 👇
A Diophantine Equation | x^2-y^2=23
Комментарии
 0:02:20
0:02:20
 0:10:57
0:10:57
 0:05:37
0:05:37
 0:05:37
0:05:37
 0:07:44
0:07:44
 0:10:57
0:10:57
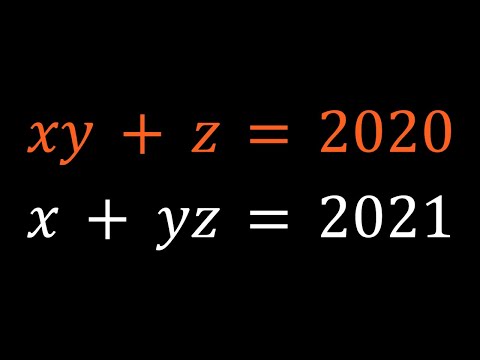 0:04:40
0:04:40
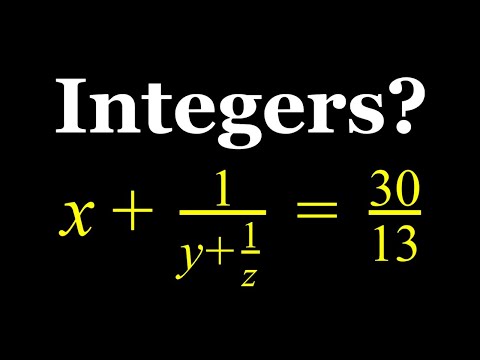 0:09:04
0:09:04
 0:15:33
0:15:33
 0:05:03
0:05:03
 0:03:30
0:03:30
 0:00:49
0:00:49
 0:01:58
0:01:58
 0:09:44
0:09:44
 0:09:12
0:09:12
 0:05:47
0:05:47
 0:16:18
0:16:18
 0:00:18
0:00:18
 0:00:37
0:00:37
 0:07:40
0:07:40
 0:04:34
0:04:34
 0:00:56
0:00:56
 0:00:35
0:00:35
 0:00:55
0:00:55