filmov
tv
n! greater than 2^n for n greater or = 4 ; Proof by Mathematical induction inequality, factorial.

Показать описание
proving n! is always greater than 2^n for all n greater or equal to 4, by the Mathematical induction.
Factorial
2 to the power of n
PMI
Factorial
2 to the power of n
PMI
Inequality Mathematical Induction Proof: 2^n greater than n^2
Induction Inequality Proof Example 5: 2^n ≥ n²
Induction: Inequality Proofs
Learn how to use mathematical induction to prove a formula
Induction Divisibility
2.3.2 Recurrence Relation Dividing [ T(n)=T(n/2)+ n]. #2
Mathematical Induction Practice Problems
1.8.1 Asymptotic Notations Big Oh - Omega - Theta #1
What does a ≡ b (mod n) mean? Basic Modular Arithmetic, Congruence
I Wish I Saw This Before Calculus
Induction Inequality Proof Example 3: 5^n + 9 less than 6^n
Prove by induction, Sum of the first n cubes, 1^3+2^3+3^3+...+n^3
L-2.4: Recurrence Relation [ T(n)= 2T(n/2) +n] | Substitution Method | Algorithm
Recursive Formulas For Sequences
Induction Inequality Proof Example 1: Σ(k = 1 to n) 1/k² ≤ 2 - 1/n
The Harmonic Number Is Never An Integer When n Is BIGGER Than 1
Limit of n!/n^n as n goes to infinity, squeeze theorem, calculus 2 tutorial
Asymptotic Analysis (Solved Problem 1)
Rearrange algebra formula to make n the subject - GCSE Question
2.1.4 Recurrence Relation T(n)=2 T(n-1)+1 #4
More and Less | Comparison for Kids | Learn Pre-School Concepts with Siya | Part 5
Series of n/2^n
1.10.1 Comparison of Functions #1
Big Oh(O) vs Big Omega(Ω) vs Big Theta(θ) notations | Asymptotic Analysis of Algorithms with Example...
Комментарии
 0:09:20
0:09:20
 0:16:15
0:16:15
 0:14:30
0:14:30
 0:07:08
0:07:08
 0:20:35
0:20:35
 0:07:26
0:07:26
 0:18:08
0:18:08
 0:15:46
0:15:46
 0:05:45
0:05:45
 0:00:43
0:00:43
 0:10:42
0:10:42
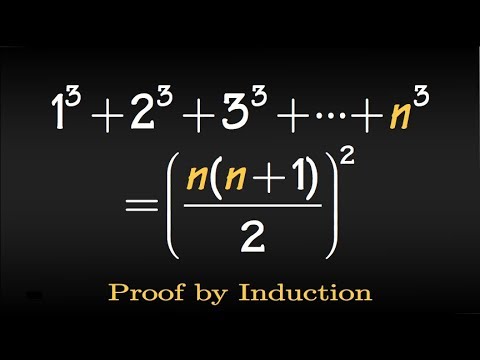 0:09:03
0:09:03
 0:08:57
0:08:57
 0:02:54
0:02:54
 0:13:09
0:13:09
 0:21:18
0:21:18
 0:10:55
0:10:55
 0:07:23
0:07:23
 0:04:50
0:04:50
 0:10:42
0:10:42
 0:01:35
0:01:35
 0:09:40
0:09:40
 0:09:28
0:09:28
 0:28:50
0:28:50