filmov
tv
Limit of n!/n^n as n goes to infinity, squeeze theorem, calculus 2 tutorial

Показать описание
limit of n!/n^n as n goes to infinity, plus the list, and squeeze theorem
Limit of n!/n^n as n goes to infinity, squeeze theorem, calculus 2 tutorial
Limit of 3^n/n! as n approaches infinity
Limit of the Sequence n!/n^n
(Squeeze Thrm) Limit n goes to Infinity n!/n^n
Limit of (n - 4)!/n!
(Limit Proofs) Lim as n goes to infinity of (1+x/n)^n
(Squeeze Thrm) Limit n goes to Infinity 7^n /n!
A Brilliant Limit
Exploring Limits: Telescoping Sum
Find the Limit of s(n) as n approaches Infinity Example
Ch4Pr12: Limit of n!/n^n
Limit with n!
Limit of (-1)^n(n/(n + 1))
A neat limit with a clever trick
Limit of sum( (1 + 4i/n)^3(8/n), i = 1,...,n ) as n approaches infinity
Find the Limit of SUM((1/n^3)(i - 1)^2) as n approaches infinity
Limit of (log n)/n as n approaches infinity
Limit at Infinity / Indeterminate form 1 to Infinity (How to find)
Limit (1-1/n)^n = 1/e as n approaches to infinity Proof |Mad Teacher
Determine the limit of the sequence {sqrt(n^2 + 3n) -n}. Multiply by conjugate
Limit of infinity of a summation example
Limit Superior and Limit Inferior Explained (with Example Problems) | Real Analysis
Finding the Limit of a Sequence, 3 more examples
(Squeeze Theorem) limit as n goes to Infinity of nth Root n
Комментарии
 0:10:55
0:10:55
 0:01:22
0:01:22
 0:01:50
0:01:50
 0:05:13
0:05:13
 0:02:41
0:02:41
 0:07:03
0:07:03
 0:05:34
0:05:34
 0:16:58
0:16:58
 0:03:31
0:03:31
 0:01:54
0:01:54
 0:04:04
0:04:04
 0:12:26
0:12:26
 0:01:20
0:01:20
 0:03:13
0:03:13
 0:07:06
0:07:06
 0:06:29
0:06:29
 0:01:51
0:01:51
 0:17:26
0:17:26
 0:01:17
0:01:17
 0:03:49
0:03:49
 0:09:35
0:09:35
 0:15:08
0:15:08
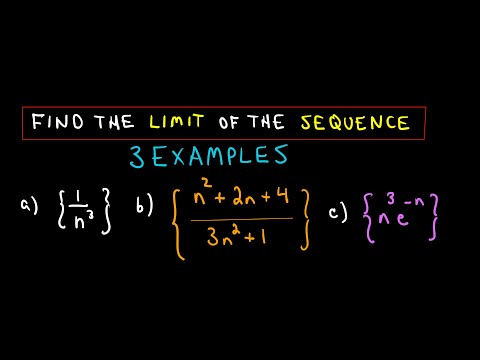 0:03:24
0:03:24
 0:06:47
0:06:47