Series of n/2^n

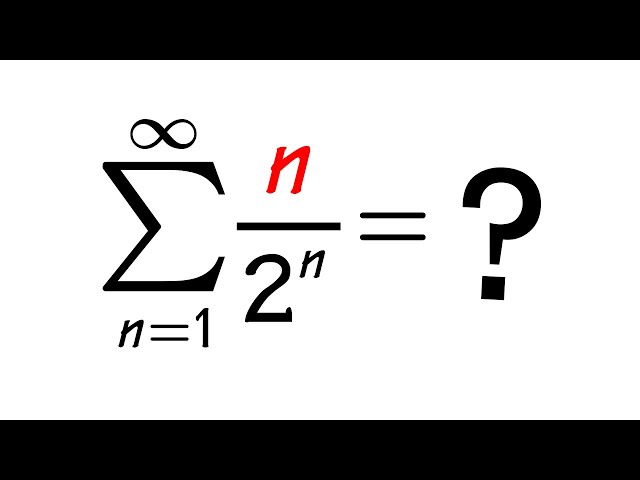
Показать описание

Рекомендации по теме

Комментарии

I will announce the 3 finalists to the video editing contest this weekend!
Get ready to enjoy their videos & vote!

100/(1-x)

blackpenredpen

Teacher : Who is your best friend ?
Me : 1/(1-x)
Teacher : Why?
Me : It squares when we differentiate it.

sarbaripanja

8:14 Both sides are divisible by 3^99. So divide both sides by 3^99 and you get a more down to earth equation. (3+3+3)/(9-3-1) or 9/5.

mrmimeisfunny

1. Using Both Pen is really cool,
2. Very informative and Clear
3. Your Smile
4. The way of showing everything.
5. i still have a problem. ( sum of the series n*2^n, where nmax= 513 and nmin = 2)

viveksidar

8:21 the answear to your little calculation is 9/5

allmight

I did it a third way, by saying {sum n=1 to infinity} ({sum k=1 to n} 1/2^n) = {sum k=1 to infinity} ({sum n=k to infinity} 1/2^n) = {sum k=1 to infinity} 1/2^(k-1) = {sum k=0 to infinity} (1/2)^k = 2

johannesh

This sum is related to Collatz conjecture.
At every step of Collatz sequence: multiplication by 3 and adding 1 produces a number with random distribution of zeros and ones (in binary representation). Then you shift right to discard all least significant zeros.
Probability of one rightmost zero is 1/2. Probability of two rightmost zeros is 1/4, three zeros 1/8, etc. On average, the shift step divides the result by 2^(1/2+2/4+3/8+4/16....)=4

To prove Collatz conjecture we only need to prove that for any starting number, the sequence always reaches a number smaller than the start. Average "reduction" being greater than 3 means the sequence is very likely to reach the smaller number.

Alexagrigorieff

Just found this channel, never thought I can look at math as being this fun!

ThunderMaster

The second method was really nice and neatly done. It all came together. I couldn't stop smiling when I figured it out just before you finished :)

Habbopingvinen

the numerator is 3(3^100), which is just 3^101. The middle term of the denominator can be written as 3^101/3 and the last term of the denominator can be written as 3^101/9. Factoring out 3^101 from the entire denominator we get 3^101(1-1/3-1/9) as the denominator. The numerator and the denominator can be simplified which leaves 1/(1-1/3-1/9) which is just 9/5.

tzakl

Picture the sum 1 + 1/2 +1/4 + 1/8 + ...
by picturing the rectangle (square) with height 1 above the interval 0 to 1 on the x-axis, a rectangle with height 1/2 above the interval 1 to 2 on the x-axis, a rectangle with height 1/4 above the interval from 2 to 3, and so on. The total area of all the rectangles is 2.

Another way to fill those same rectangles is to add the rectangles:
1/2 <= y <= 1 for 0 <= x <=1,
1/4 <= y <= 1/2 for 0 <= x <=2,
1/8 <= y <= 1/4 for 0 <= x <=3,
1/16 <= y <= 1/8 for 0 <= x <=4, etc.
These rectangles have area 1×1/2 + 2×1/4 + 3×1/8 + 4×1/16 + ...
and must also sum to 2.

dr_rich_r

Calculus BC Teacher: WE ARE GONNA REVIEW SERIES!!
me: noooo
blackpenredpen: dont worry...

JaydentheMathGuy

Just messed up my Calculus exam, going to have to do a resit, never thought watching math videos would cheer me up :)

VOMotion

I like your utilisation of the best friend, very cool!

teekak

Question at the end: Just factor out 3^99 on top and bottom. Then you get (3+3+3)/(9-3-1) = 9/5. Easy.

hi

Similar to 1/2+1/4+1/8...series.
I made a formula generalising n, and also n.

anonymousunknown

I solved it by writing n = n-1 + 1
I get sum from n=1 to inf (n-1)/2^n + sum n=1 to inf 1/2^n
The first is equal to 1/2 of the original sum, and the second is equal to 1
Letting S equals the original sum I get S = 1/2S + 1 => 1/2S = 1 => S = 2

SciDiFuoco

I think this can be generalized to arbitrary (arithmetic series)_n / (geometric series)_n.
Say, S=a_1 + a_2*q +a_3*q^2 +...+a_n*q^(n-1),
then qS=a_1*q +a_2*q^2 + a_3*q^3 +...+a_n*q^n ;
S-qS=a_1 + (a_2-a_1)q + (a_3-a_2)q^2 +...+(a_n - a_[n-1] )q^(n-1) - a_n*q^n .
We know that a_n - a_[n-1] = d (the difference) and we can factor it out. The middle part is then d*(q +q^2 +...+q^(n-1) ) - just a geometric series, its sum is dq/(1-q), if |q|<1, in the limit n->inf . Also we know that a_n=a_1 + d(n-1), so the last term splits into two: a_1*q^n and d*(n-1)*q^n. The first of these obviously goes to zero in the limit, the second goes to zero also, but L'hopital's rule is needed to show that.
Finally, we are left with
S-qS=a_1 +dq/(1-q) ;
S=a_1/(1-q) +dq/(1-q)^2.
If the geometric series doesn't start at 1, we can always factor that first term out, thus:
if S=sum[n=1, n->inf] (a_1*b*q^(n-1) ), then
S=a_1*b/(1-q) +dqb/(1-q)^2 ;
in our case a_1=1, b=1/2, q=1/2, d=1 ;
S=1*0.5/0.5 +1*0.5*0.5/(0.5)^2 = 1 + 1 = 2.

Hexanitrobenzene

som from n=1 to if of (n/b^n) = b/(b-1)^2 b€R\(-1, 1) you can easily prove it for every b if you replace 2 with b if you do the classical way, then you can test for which b it converges

pawelszewczenko

1:23 A.M. here and nothing feels more fun than math❤️

amirparsi

Series of n/2^n

Series of n/2^n

Sum of n/2^n

Infinite Series Convergence and Divergence Example with SUM((2n)!/(n!)^2) Ratio Test

series of n/2^n as a double summation

Convergence and Divergence - Introduction to Series

Find the Sum of the Series SUM((2^n + 1)/3^n)

checking for absolute convergence, series of sin(2n)/(1+2^n), calculus 2 tutorial

Series of (2n+1)^n/(n^(2n)) by the Root Test, calculus 2 tutorial

Find sum of series {2^(2n +1)/5^n}. Geometric Series

Telescoping Series

know the series of n!/e^(n^2) for your final exam, ratio test!

Calculus 2 - Geometric Series, P-Series, Ratio Test, Root Test, Alternating Series, Integral Test

Determine if series converges or diverges, if converges find limit {3^(n+2)/(5^n)}.

If I did this in 1734 I'd be World Famous

Determine if series is absolutely, conditionally convergent or divergent { (-2)^n/(n ln n) }

Proof by Induction : Sum of series ∑r² | ExamSolutions

100 series convergence tests (no food, no water, no stop)

Sum of the Infinite Geometric Series starting at n = 2: SUM(2(1/3)^n) #shorts

Determine whether series converges or diverges (sqrt(n))/(n^2 +1). Use appropriate test

Series of (1+1/n)^(n^2), root test

Alternating Series of (-1)^n*n/(n+2), calculus 2 tutorial

Determine if series converges or diverges, if converges find limit {n^2/(sqrt(n^3 + 4n))}

series of n^2*e^(-n^3) by using the integral test, calculus 2 tutorial

Determine if series converges or diverges. {(cos^2 n)/(n^2 +1)}. Comparison Test with P-series