filmov
tv
📐How to Find The Area of the Triangle ? | 2 Methods

Показать описание
In this lesson, we learned two methods to find the area of a triangle. We used the sine area formula and also applied the concept of similar triangles. Additionally, we made use of information about quadratic equations.
Don't forget to subscribe and turn on the notification bell! :)
Thank you for watching.
#geometry #math #triangles
Don't forget to subscribe and turn on the notification bell! :)
Thank you for watching.
#geometry #math #triangles
Math Antics - Area
How to Find the Area of a Rectangle | Math with Mr. J
Finding the Area of a Composite Figure | Area of Composite Rectangles
How to Find Area | Rectangles, Squares, Triangles, & Circles | Math Mr. J
How to Find the Area of a Square | Math with Mr. J
Area for Kids
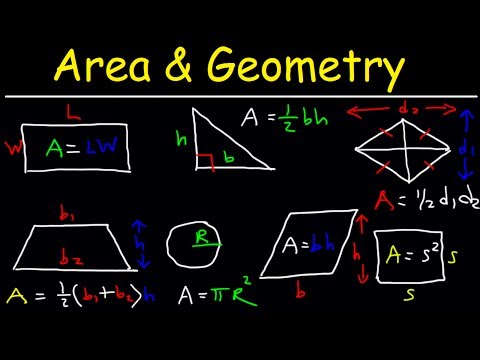
Area of a Rectangle, Triangle, Circle & Sector, Trapezoid, Square, Parallelogram, Rhombus, Geome...
Finding the Area of a Triangle | A Step-By-Step Guide | Math with Mr. J
How to Find the Area of a Circle | Area of a Circle Step by Step
How to Find the Area and Perimeter of a Triangle | Math with Mr. J
Area & Perimeter of a Triangle
Area and perimeter of square | Ayushi teacher | Area and perimeter #maths #area #perimeter
Area of the figure | Area of the rectangle | #mathstricks #shorts
Area of a Trapezoid (Trapezium) | Math with Mr. J
Area of square | How to find area of the square #shorts
Area and Perimeter
How to Find the Area of a Triangle | Calculate the Area of a Triangle
Area of a Square | MathHelp.com
How to Find the Area of Rectangles and Squares | Math with Mr. J
Area of a Triangle | MathHelp.com
Find the Area Challenge
Finding the Perimeter
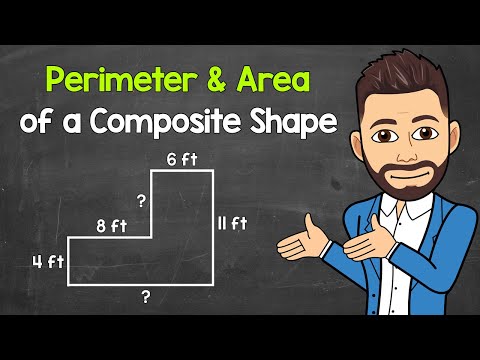
Finding the Perimeter and Area of a Composite Shape | L-Shaped Example | Geometry | Math with Mr. J
Area of a Circle | MathHelp.com
Комментарии
 0:10:26
0:10:26
 0:04:43
0:04:43
 0:07:14
0:07:14
 0:22:10
0:22:10
 0:02:48
0:02:48
 0:08:58
0:08:58
 0:20:35
0:20:35
 0:07:35
0:07:35
 0:06:39
0:06:39
 0:05:48
0:05:48
 0:00:16
0:00:16
 0:00:16
0:00:16
 0:00:48
0:00:48
 0:06:14
0:06:14
 0:00:30
0:00:30
 0:17:49
0:17:49
 0:06:37
0:06:37
 0:01:14
0:01:14
 0:06:57
0:06:57
 0:01:36
0:01:36
 0:04:33
0:04:33
 0:00:40
0:00:40
 0:08:21
0:08:21
 0:01:40
0:01:40