filmov
tv
Solving An Interesting Log Equation | Math Olympiads
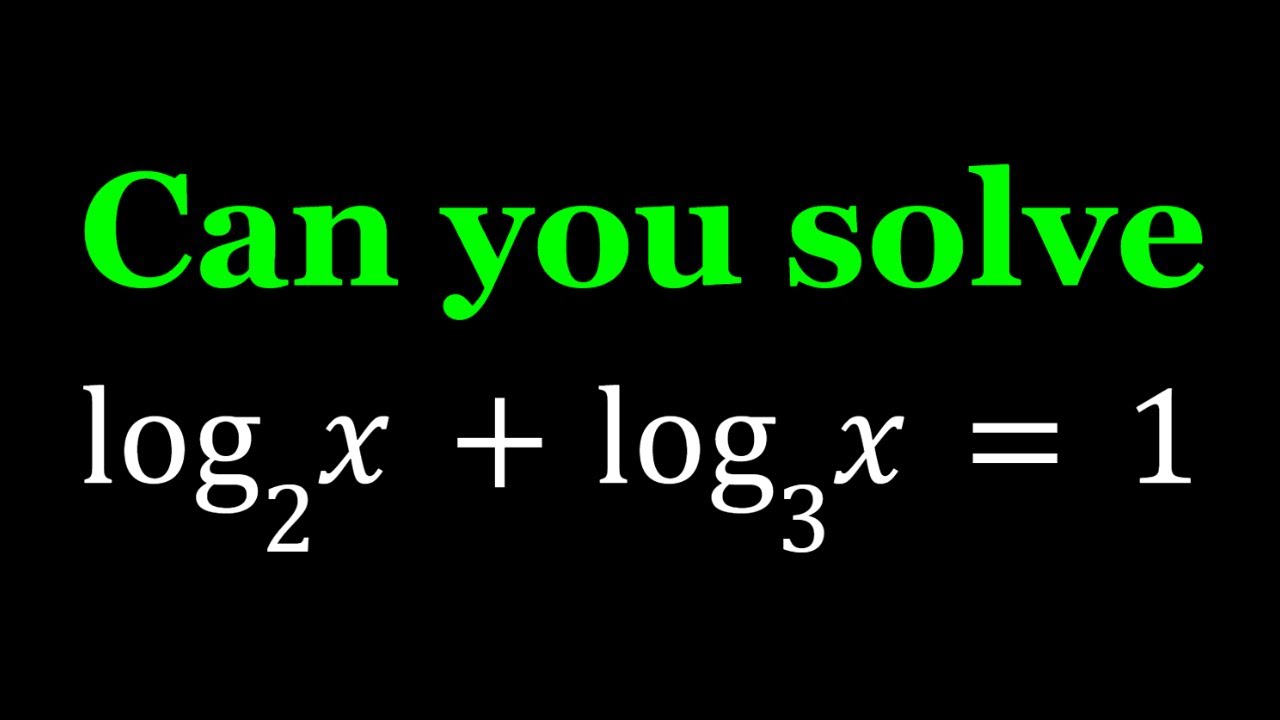
Показать описание
🤩 Hello everyone, I'm very excited to bring you a new channel (SyberMath Shorts)
Enjoy...and thank you for your support!!! 🧡🥰🎉🥳🧡
If you need to post a picture of your solution or idea:
#ChallengingMathProblems #LogarithmicEquations #Logarithms
via @YouTube @Apple @Desmos @NotabilityApp @googledocs @canva
PLAYLISTS 🎵 :
Enjoy...and thank you for your support!!! 🧡🥰🎉🥳🧡
If you need to post a picture of your solution or idea:
#ChallengingMathProblems #LogarithmicEquations #Logarithms
via @YouTube @Apple @Desmos @NotabilityApp @googledocs @canva
PLAYLISTS 🎵 :
Solving Logarithmic Equations
Solving An Interesting Log Equation | Math Olympiads
Solving logarithmic equations | Exponential and logarithmic functions | Algebra II | Khan Academy
Solving Exponential and Logarithmic Equations
solving a logarithmic equation with different bases
Solving logarithmic equations by factoring
Solving Log Equation
Solving Logarithmic Equations... How? (NancyPi)
Why I don't like using Lambert W function to solve exponential equation
SOLVING LOGARITHMIC EQUATIONS || FINDING THE VALUE OF X
solving a logarithmic equation with different bases
Solving Log Equations (Pre Calc)
Solving (Challenging) Log Equations Different Bases
Solving Complex Logarithmic Equations
Solving Logarithmic Equations | Logarithm | Laws of Logarithm | General Mathematics
04 - Solving Logarithmic Equations - Part 1 - Equations with Log(x)
Using one to one property to solve logarithmic equation
Solving logarithmic equations
Solving Exponential and Logarithmic Equations (Multiple Examples)
Solving an logarithmic equation
Solving a Log Equation with Different Bases
How to Solve Exponential Equations using Logarithms - No Common Base Present
Ex: Solve Logarithmic Equations Containing Only Logarithms
Solving a logarithmic equation with no solutions
Комментарии
 0:25:27
0:25:27
 0:09:47
0:09:47
 0:04:13
0:04:13
 0:07:08
0:07:08
 0:06:02
0:06:02
 0:07:00
0:07:00
 0:00:55
0:00:55
 0:15:05
0:15:05
 0:03:32
0:03:32
 0:14:27
0:14:27
 0:04:10
0:04:10
 0:09:18
0:09:18
 0:02:50
0:02:50
 0:10:42
0:10:42
 0:13:29
0:13:29
 0:27:26
0:27:26
 0:04:42
0:04:42
 0:00:57
0:00:57
 0:12:27
0:12:27
 0:06:41
0:06:41
 0:08:47
0:08:47
 0:05:47
0:05:47
 0:05:18
0:05:18
 0:03:36
0:03:36