filmov
tv
Real Analysis | The Cauchy Condensation Test
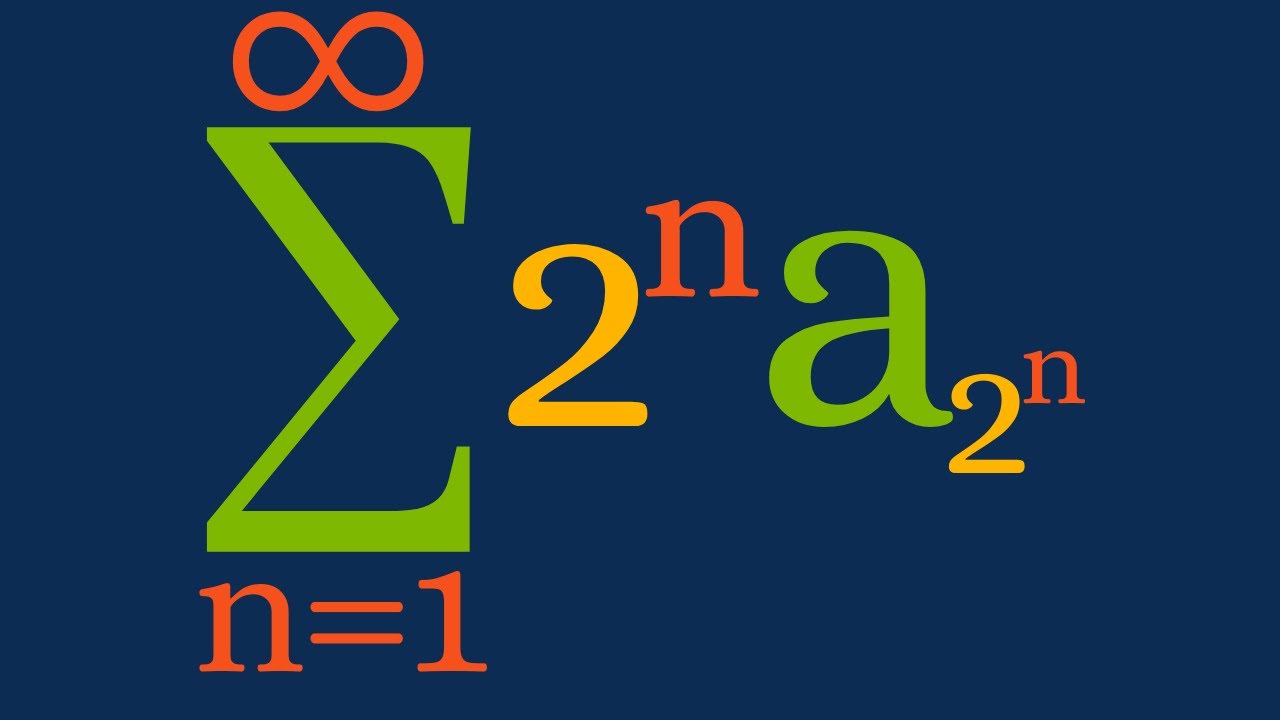
Показать описание
We prove a series convergence test known as the Cauchy condensation test. This test is motivated by the classic proof of the divergence of the harmonic series.
If you are going to use an ad-blocker, considering using brave and tipping me BAT!
Books I like:
Abstract Algebra:
Differential Forms:
Number Theory:
Analysis:
Calculus:
If you are going to use an ad-blocker, considering using brave and tipping me BAT!
Books I like:
Abstract Algebra:
Differential Forms:
Number Theory:
Analysis:
Calculus:
Intro to Cauchy Sequences and Cauchy Criterion | Real Analysis
Real Analysis | Cauchy Sequences
Real Analysis 7 | Cauchy Sequences and Completeness
Real Analysis 17 | Cauchy Criterion
Proof: Sequence is Cauchy if and only if it Converges | Real Analysis
Real Analysis | The Cauchy Condensation Test
Real Analysis 22 | Cauchy Product
Real Analysis 64 | Cauchy Principal Value
Proof: Sequence (1/n) is a Cauchy Sequence | Real Analysis Exercises
Proof: Cauchy Sequences are Convergent | Real Analysis
Real Analysis 7 | Cauchy Sequences and Completeness [dark version]
Proof: Cauchy Sequences are Bounded | Real Analysis
Proof: Convergent Sequences are Cauchy | Real Analysis
Sequences (Real Analysis) | Cauchy Sequences | Lecture 7 | Cauchy convergence criteria
Real Analysis I (lec 1.2.A) Cauchy Sequences
Real Analysis 22 | Cauchy Product [dark version]
Real Analysis 17 | Cauchy Criterion [dark version]
Real Analysis | Cauchy Criterion for Series
Real Analysis | Cauchy Sequence | Cauchy Sequence Example & Definition
Idea of Proof of the Cauchy-Schwarz Inequality
T.Y.B.Sc(Real Analysis) || Topic: Cauchy's Root Test || By Prof. Andhare P.G.
Visual Cauchy-Schwarz Inequality
Cauchy Sequence | Easy lecture 11 | Real Analysis
Real Analysis-Sequences-14:Cauchy Sequences
Комментарии
 0:15:53
0:15:53
 0:19:15
0:19:15
 0:09:14
0:09:14
 0:09:17
0:09:17
 0:24:23
0:24:23
 0:13:47
0:13:47
 0:08:23
0:08:23
 0:09:16
0:09:16
 0:08:16
0:08:16
 0:11:35
0:11:35
 0:09:01
0:09:01
 0:05:33
0:05:33
 0:05:45
0:05:45
 0:04:50
0:04:50
 0:01:35
0:01:35
 0:08:09
0:08:09
 0:09:04
0:09:04
 0:14:38
0:14:38
 0:15:01
0:15:01
 0:14:39
0:14:39
 0:44:15
0:44:15
 0:01:01
0:01:01
 0:03:03
0:03:03
 0:18:06
0:18:06