filmov
tv
Abstract Algebra | Units and zero divisors of a ring.
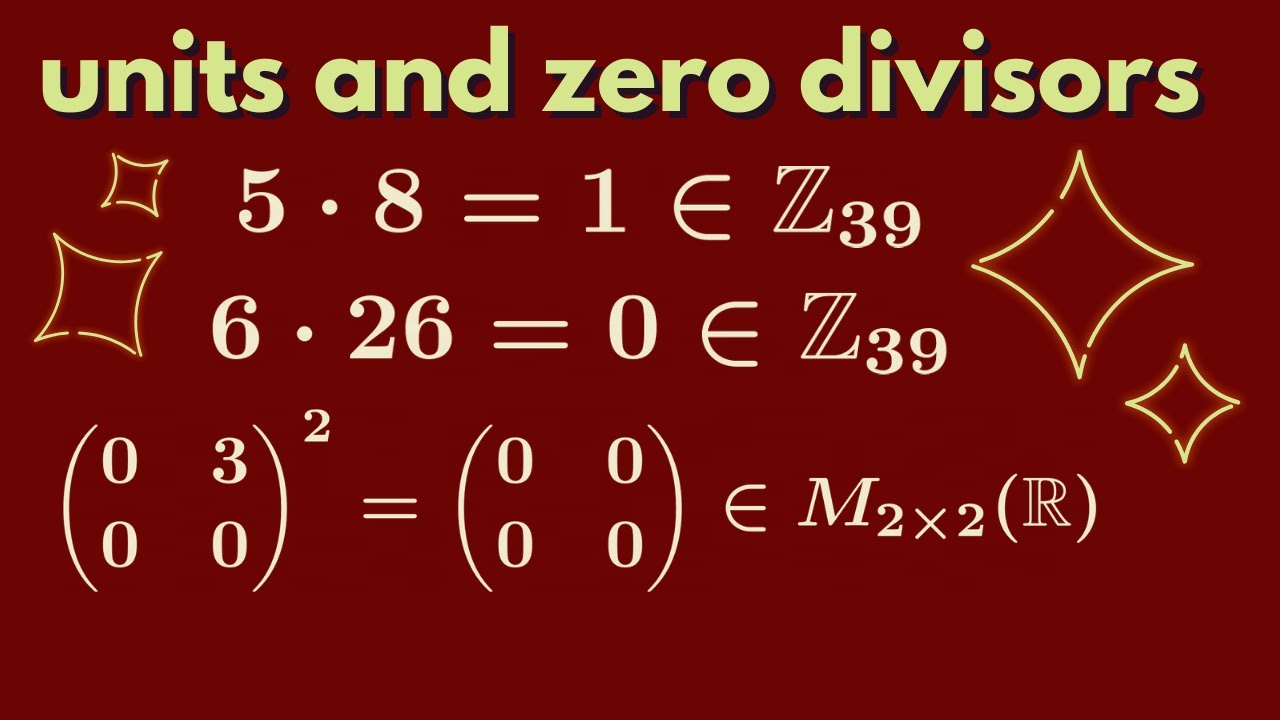
Показать описание
We classify the units and zero divisors of Zn and the ring of 2x2 matrices with real entries.
(Abstract Algebra 1) Units Modulo n
Units in a Ring (Abstract Algebra)
(Abstract Algebra 1) Definition of a Cyclic Group
Abstract Algebra | Units and zero divisors of a ring.
Abstract Algebra | Group of Units modulo n
Algebraic Structures: Groups, Rings, and Fields
(Abstract Algebra 1) Definition of a Group
Groups of units U(n) under multiplication modulo n
EVERY FINITE INTEGRAL DOMAIN IS A FIELD/ABSTRACT ALGEBRA/ MATHS/
Abstract Algebra | What is a ring?
An introduction to abstract algebra | Abstract Algebra Math Foundations 213 | NJ Wildberger
Abstract Algebra: Group of Units, Integral Domains, Fields, Polynomial Ring Examples & Calculati...
Abstract Algebra for Beginners #mathematics #math
Ring Definition (expanded) - Abstract Algebra
Abstract Algebra | Introduction to Unique Factorization Domains
Group Definition (expanded) - Abstract Algebra
Field Theory | Definition & Example Of Field | Unit Element in Ring | Abstract Algebra
Advanced Abstract Algebra || Unit 1st || Msc Maths 2nd Sem || Module theory #msc
Abstract Algebra 1, unit 1, unit 2, unit 3, unit 4, sem 2, MSC/MA, full notes, hnbgu university
Abstract Algebra - 8.2 Groups of Units Modulo n as External Direct Products
Ring Theory-Units in a polynomial Ring
Groups of units modulo n||Un group in group theory || Group theory
Contemporary Abstract Algebra by Joseph Gallian #shorts
Abstract Algebra, Lec 24B: Subrings, Subring Test, Groups of Units, Integral Domains, Fields
Комментарии
 0:15:25
0:15:25
 0:07:14
0:07:14
 0:09:01
0:09:01
 0:22:49
0:22:49
 0:09:02
0:09:02
 0:23:42
0:23:42
 0:12:25
0:12:25
 0:17:49
0:17:49
 0:07:29
0:07:29
 0:08:52
0:08:52
 0:25:38
0:25:38
 0:59:11
0:59:11
 0:01:00
0:01:00
 0:06:51
0:06:51
 0:11:08
0:11:08
 0:11:15
0:11:15
 0:19:11
0:19:11
 0:00:46
0:00:46
 0:03:21
0:03:21
 0:07:42
0:07:42
 0:02:58
0:02:58
 0:13:10
0:13:10
 0:00:16
0:00:16
 0:29:10
0:29:10