filmov
tv
Trigonometric Class 11 | Chinese Math Olympiad Question.
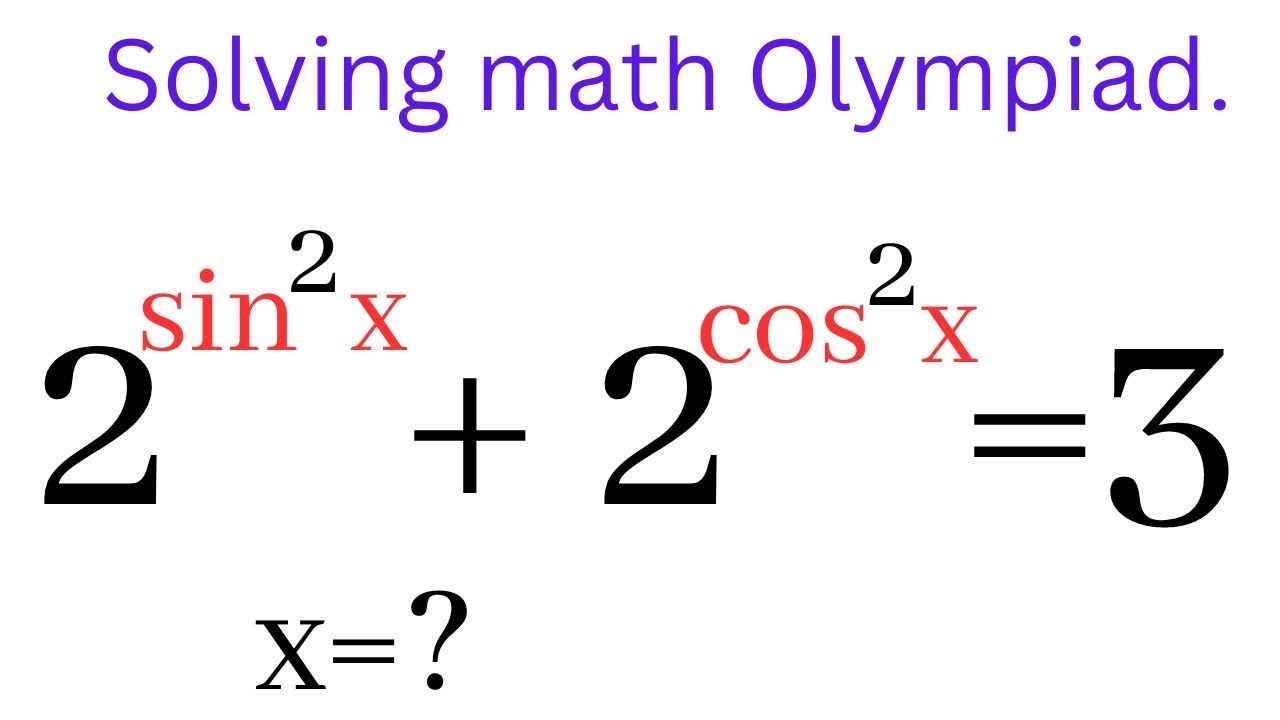
Показать описание
In this tutorial, you will learn how to solve this trigonometric class 11 challenge from math Olympiad competition by applying one of the major trigonometric identities.
I will equally guide you on how to get other possible values of x from the unit circle when x turns or rotates more than 360 degrees.
Leave a comment in the comment sections just to know your take or view about the approach to solving this math challenge.
Also do not forget to like and share this wonderful video tutorial using the link below.
Do you know that you can gain more subscribers and have more views using Promoterskit?. Check in the link below to grew your YouTube channel in a short period of time.
Many thanks to all our subscribers and viewers all over the world, we love and cherish you all deeply as far this channel is concerned 💕💕❤️❤️🎉🎉🎉🙏🙏🙏
Best regards from OnlineMathsTV.
#howto #maths #olympiadexams
I will equally guide you on how to get other possible values of x from the unit circle when x turns or rotates more than 360 degrees.
Leave a comment in the comment sections just to know your take or view about the approach to solving this math challenge.
Also do not forget to like and share this wonderful video tutorial using the link below.
Do you know that you can gain more subscribers and have more views using Promoterskit?. Check in the link below to grew your YouTube channel in a short period of time.
Many thanks to all our subscribers and viewers all over the world, we love and cherish you all deeply as far this channel is concerned 💕💕❤️❤️🎉🎉🎉🙏🙏🙏
Best regards from OnlineMathsTV.
#howto #maths #olympiadexams
Trigonometric Class 11 | Chinese Math Olympiad Question.
Oxford student reacts to India’s JEE Advanced exam paper *really hard* #shorts #viral #jeeadvanced
HOW CHINESE STUDENTS SO FAST IN SOLVING MATH OVER AMERICAN STUDENTS
when calculus students use trig identities too early
a trig identities song???
🤯 This ONE CIRCLE will make you finally understand trigonometry #shorts
Human Calculator Solves World’s Longest Math Problem #shorts
Bill Gates Vs Human Calculator
Questions I get as a human calculator #shorts
2022 China Math Olympiad: A Trigonometry Problem (fill-in-the-blank problem)
Oxford Student reacts to China’s INSANELY DIFFICULT High School GaoKao Maths paper #shorts #viral
You're a physicist, so you're good at math, right? #Shorts
2022 China Math Olympiad: A Trigonometry Problem tan(x-y) (fill-in-the-blank problem)
How to remember trigonometry formulas 😂🕺🏻💃🏻 #igcse #addmaths #malaysia #maths #funnyshorts...
When mathematicians get bored (ep1)
That's Why Mohit Sir Called 'God Of Mathematics'| Puzzle Brain teaser | #competishun ...
Why greatest Mathematicians are not trying to prove Riemann Hypothesis? || #short #terencetao #maths
The Hardest Math Test
Maths vs Physics
Memorization Trick for Graphing Functions Part 1 | Algebra Math Hack #shorts #math #school
Invading a first year Maths lecture #shorts #tiktokviral #oxforduniversity
👀 Asking GCSE Students (Hamdi) How Much They Physics They Know - Part 1 #Shorts
Redefining the Trig Functions on the Unit Circle (1 of 2: The Basic Concept)
Where do Sin, Cos and Tan Actually Come From - Origins of Trigonometry - Part 1
Комментарии
 0:15:13
0:15:13
 0:01:00
0:01:00
 0:00:23
0:00:23
 0:00:43
0:00:43
 0:00:26
0:00:26
 0:01:00
0:01:00
 0:00:34
0:00:34
 0:00:51
0:00:51
 0:00:16
0:00:16
 0:01:00
0:01:00
 0:00:59
0:00:59
 0:00:09
0:00:09
 0:00:53
0:00:53
 0:00:37
0:00:37
 0:00:37
0:00:37
 0:00:19
0:00:19
 0:00:38
0:00:38
 0:00:28
0:00:28
 0:00:25
0:00:25
 0:00:15
0:00:15
 0:01:00
0:01:00
 0:00:37
0:00:37
 0:10:53
0:10:53
 0:09:15
0:09:15