filmov
tv
Introduction to Quantum Mechanics: Schrodinger Equation

Показать описание
There's no better way to celebrate Christmas than with a 12 minute video on the Schrodinger Equation! In this lesson, I introduce Quantum Mechanics with a discussion on wavefunctions and the Schrodinger Equation (in 1-D). I show how wavefunctions can represent probability density functions (via the norm-squared), and discuss the significance of this representation.
I then introduce/revisit some basic Statistics concepts, and end the video with a proof of how the normalization of wavefunctions stays preserved with time.
Questions/requests? Ask in the comments!
Special thanks to my Patrons:
- Jennifer Helfman
- Justin Hill
- Jacob Soares
- Yenyo Pal
- Lisa Bouchard
NOTE: At around 11:30-11:45, I mention how the 'boundary' integrals have to approach zero at +/- infinity. This is true for square-integrable functions that come up in Physics. However, as one of the commenters pointed out, there are exceptions (i.e. square-integrable functions that don't approach zero at infinity). These exceptions aren't found in Physics though, so we'll ignore them, but I figure they're worth mentioning as a footnote.
I then introduce/revisit some basic Statistics concepts, and end the video with a proof of how the normalization of wavefunctions stays preserved with time.
Questions/requests? Ask in the comments!
Special thanks to my Patrons:
- Jennifer Helfman
- Justin Hill
- Jacob Soares
- Yenyo Pal
- Lisa Bouchard
NOTE: At around 11:30-11:45, I mention how the 'boundary' integrals have to approach zero at +/- infinity. This is true for square-integrable functions that come up in Physics. However, as one of the commenters pointed out, there are exceptions (i.e. square-integrable functions that don't approach zero at infinity). These exceptions aren't found in Physics though, so we'll ignore them, but I figure they're worth mentioning as a footnote.
Комментарии
 1:27:34
1:27:34
 0:06:28
0:06:28
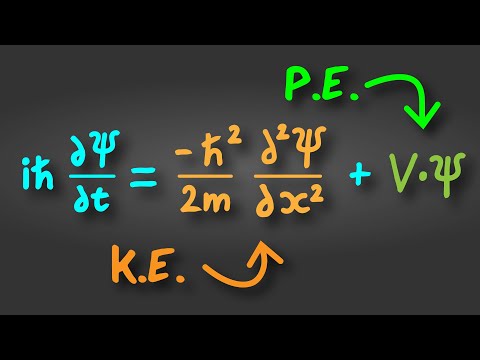 0:01:00
0:01:00
 0:04:38
0:04:38
 0:12:38
0:12:38
 0:01:22
0:01:22
 0:56:11
0:56:11
 0:06:34
0:06:34
 0:00:48
0:00:48
 0:07:47
0:07:47
 0:10:11
0:10:11
 0:09:28
0:09:28
 0:18:35
0:18:35
 0:08:45
0:08:45
 1:23:14
1:23:14
 0:04:19
0:04:19
 3:32:45
3:32:45
 0:05:42
0:05:42
 0:22:22
0:22:22
 0:07:41
0:07:41
 0:12:03
0:12:03
 0:11:19
0:11:19
 0:17:54
0:17:54
 1:22:19
1:22:19