filmov
tv
Find the Red Area Area
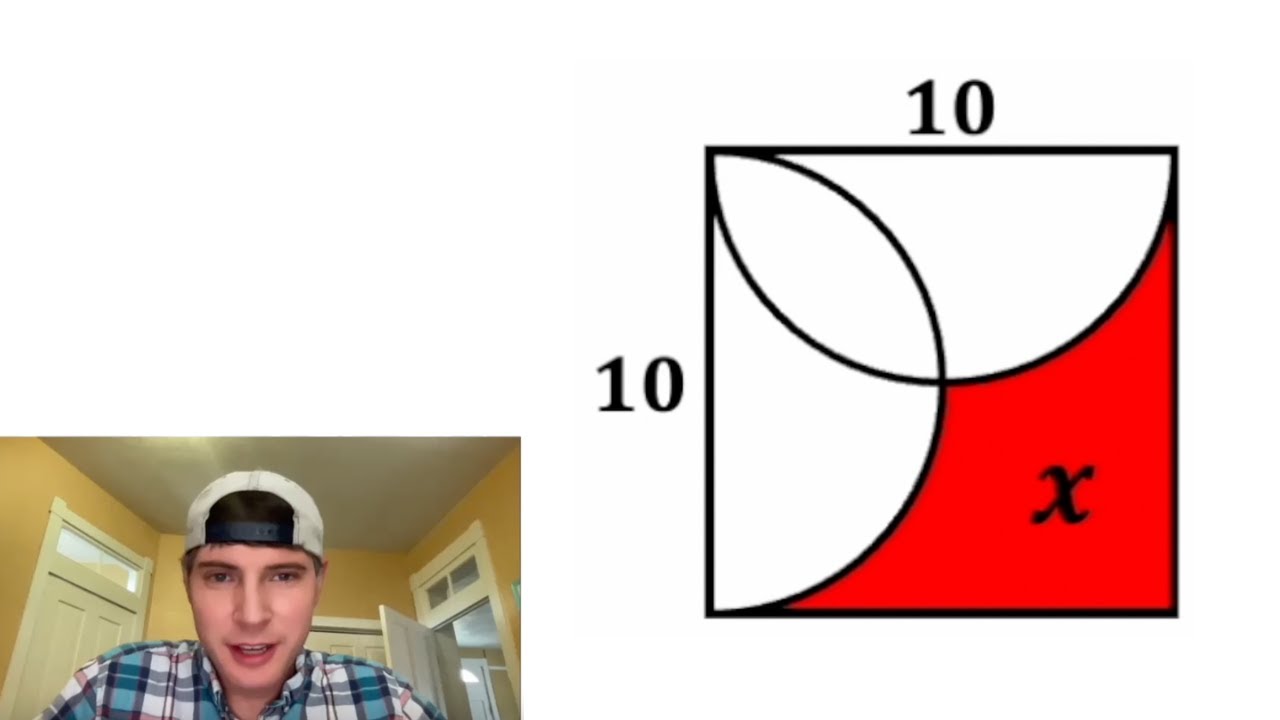
Показать описание
Find the Red Area Area
Area of Red Triangle
Find Area of Red Region
Find the area of the red region.
Can You Find the Red Area Under the Curve? Test Your Math Skills Part 10
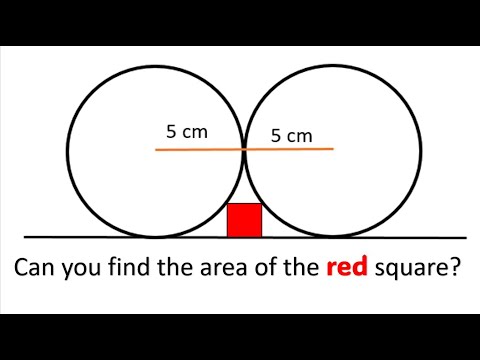
Find the Area of the Red Square - Geometry Challenge Problem
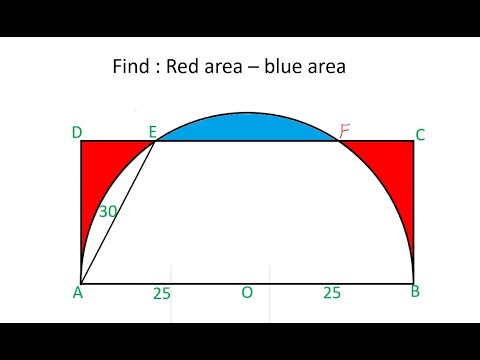
Find the difference of areas of Red region and blue region
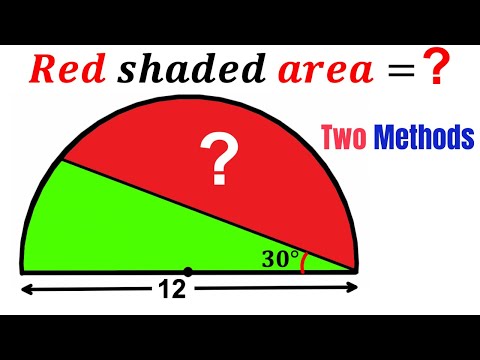
Can you find area of the Red shaded region? | (2 Methods) | #math #maths | #geometry
MW3 ZOMBIES : JAK DEVASTATORS DUAL RECLAIMER 18 in RED ZONE and NEW DARK AETHER ELDER SIGIL #mwz
Find the Area of the Red Shaded Quadrant | Step-by-Step Explanation
Can You Find the Red Area Above the Curves Inside the Rectangle? Test Your Math Skills Part 15
Find Perimeter of Red Area | Important Geometry Skills | A Nice Problem of Geometry
How to calculate the red area in this Trapezium? | Learn the simple and easy trick to solve
Geometry | Finding the Area of the Red Shaded Right Triangle
Area of Red Triangle
Can You Find the Red Area Inside the Circle? Test Your Math Skills Part 28
Geometry: Calculating the Area of Shaded Red Region | Circle Inside Quarter Circle
patna red light area//#part5 ladki dekh aapko raha nahi jaayega 💯💦
Find the Area of the Red Square in Between 2 Circles | Step-by-Step Explanation
Olympiad Mathematics | Can you find the Red region area? | (Simple explanation) | #math #maths
Tricky Geometry Challenge: Find the red area!
Fun Geometry Problem | Find Area of Red Region #geometry #maths
In-depth explanation | Can you find area of the Red shaded triangle? | #math #maths #mathematics
Can You Find the Red Area in This Square? Test Your Math Skills Part 8
Комментарии
 0:01:40
0:01:40
 0:03:35
0:03:35
 0:03:27
0:03:27
 0:03:43
0:03:43
 0:05:47
0:05:47
 0:04:13
0:04:13
 0:05:43
0:05:43
 0:10:59
0:10:59
 0:31:05
0:31:05
 0:12:35
0:12:35
 0:14:10
0:14:10
 0:09:37
0:09:37
 0:02:47
0:02:47
 0:11:02
0:11:02
 0:02:07
0:02:07
 0:14:51
0:14:51
 0:04:23
0:04:23
 0:00:24
0:00:24
 0:12:34
0:12:34
 0:09:49
0:09:49
 0:05:48
0:05:48
 0:10:16
0:10:16
 0:08:09
0:08:09
 0:03:17
0:03:17