filmov
tv
Linear Transformations -- Abstract Linear Algebra 13

Показать описание
⭐Support the channel⭐
⭐my other channels⭐
⭐My Links⭐
⭐my other channels⭐
⭐My Links⭐
Linear Transformations -- Abstract Linear Algebra 13
Linear Transformations -- Abstract Linear Algebra 8
Linear Transformations on Vector Spaces
Abstract vector spaces | Chapter 16, Essence of linear algebra
Linear transformations | Matrix transformations | Linear Algebra | Khan Academy
Linear transformations and matrices | Chapter 3, Essence of linear algebra
Oxford Linear Algebra: Linear Transformations Explained
Dear linear algebra students, This is what matrices (and matrix manipulation) really look like
Linear Transformations
How to Find the Matrix of a Linear Transformation
Abstract Vector Spaces, Subspaces, Linear Transformations, Kernel, Image, One to One and Onto LTs
Linear Algebra: 015 Linear Transformations III More on Rank, Direct Sums, Matrix Transformations
Transformation matrix with respect to a basis | Linear Algebra | Khan Academy
Find the Image of a Linear Transformation
[Linear Algebra] Linear Transformations
Linear Transformations in Practice - Linear Algebra - M4
Abstract Algebra 59: Analogy between group homomorphisms and linear transformations (linear algebra)
Change of basis | Chapter 13, Essence of linear algebra
Linear Algebra 4.2.3 Linear Transformations
Matrix Representations of Linear Transformation
Image and Kernel
Isomorphism
Nilpotent Linear Transformation || Index of Nilpotence of a Linear Transformation
Gilbert Strang: Linear Algebra vs Calculus
Комментарии
 0:25:07
0:25:07
 0:34:34
0:34:34
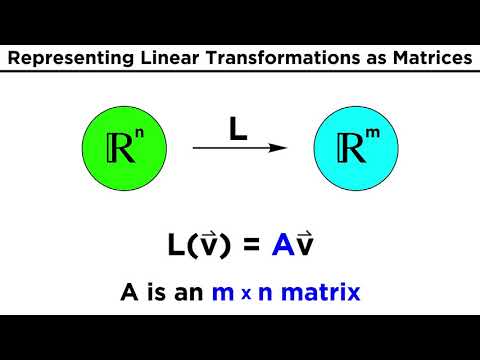 0:09:11
0:09:11
 0:16:46
0:16:46
 0:13:52
0:13:52
 0:10:59
0:10:59
 0:32:58
0:32:58
 0:16:26
0:16:26
 0:10:47
0:10:47
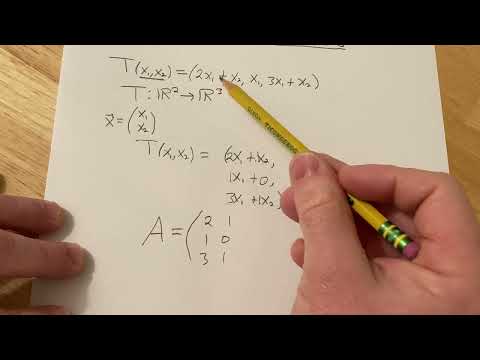 0:05:19
0:05:19
 0:45:23
0:45:23
 0:55:36
0:55:36
 0:18:02
0:18:02
 0:12:10
0:12:10
![[Linear Algebra] Linear](https://i.ytimg.com/vi/cFIRXQBfgg0/hqdefault.jpg) 0:12:30
0:12:30
 0:31:32
0:31:32
 0:14:08
0:14:08
 0:12:51
0:12:51
 0:08:48
0:08:48
 0:13:08
0:13:08
 0:05:35
0:05:35
 0:12:51
0:12:51
 0:11:57
0:11:57
 0:02:14
0:02:14