filmov
tv
Linear Transformations

Показать описание
MIT 18.06SC Linear Algebra, Fall 2011
Instructor: Nikola Kamburov
A teaching assistant works through a problem on linear transformations.
License: Creative Commons BY-NC-SA
Instructor: Nikola Kamburov
A teaching assistant works through a problem on linear transformations.
License: Creative Commons BY-NC-SA
Linear transformations and matrices | Chapter 3, Essence of linear algebra
Linear transformations | Matrix transformations | Linear Algebra | Khan Academy
Linear Transformations on Vector Spaces
Three-dimensional linear transformations | Chapter 5, Essence of linear algebra
Linear Transformations , Example 1, Part 1 of 2
Linear Algebra 1.8.2 Introduction to Linear Transformations
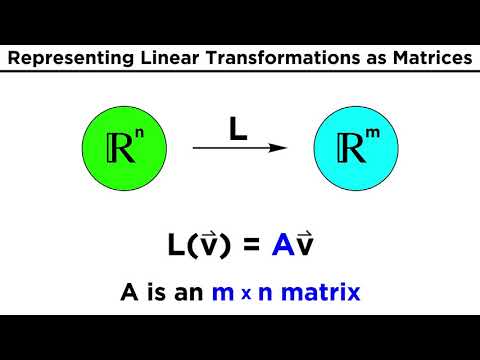
How to Find the Matrix of a Linear Transformation
Linear Transformations
Introduction to Lie Algebras | Dr. S. Ilangovan | RKMVERI, Belur Math | Talk 2
Matrix Transformations and Linear Transformations | Linear Algebra
Oxford Linear Algebra: Linear Transformations Explained
[Linear Algebra] Linear Transformations
Linear Algebra 1.8.1 Matrix Transformations
Linear Transformations
Linear Algebra - Lecture 17 - Matrix Transformations
Linear transformation examples: Rotations in R2 | Linear Algebra | Khan Academy
Linear transformation examples: Scaling and reflections | Linear Algebra | Khan Academy
Change of basis | Chapter 13, Essence of linear algebra
Linear Transformations
Linear Algebra - Lecture 19 - The Matrix of a Linear Transformation
Proving a Function is a Linear Transformation F(x,y) = (2x + y, x - y)
Matrix multiplication as composition | Chapter 4, Essence of linear algebra
Cross products in the light of linear transformations | Chapter 11, Essence of linear algebra
Linear Algebra - Lecture 18 - Linear Transformations
Комментарии
 0:10:59
0:10:59
 0:13:52
0:13:52
 0:09:11
0:09:11
 0:04:46
0:04:46
 0:09:06
0:09:06
 0:09:23
0:09:23
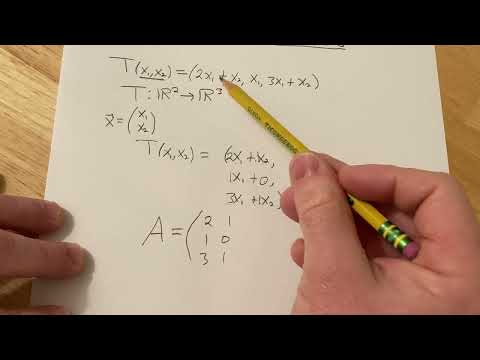 0:05:19
0:05:19
 0:10:47
0:10:47
 1:06:55
1:06:55
 0:16:01
0:16:01
 0:32:58
0:32:58
![[Linear Algebra] Linear](https://i.ytimg.com/vi/cFIRXQBfgg0/hqdefault.jpg) 0:12:30
0:12:30
 0:13:49
0:13:49
 0:11:22
0:11:22
 0:11:32
0:11:32
 0:17:52
0:17:52
 0:15:13
0:15:13
 0:12:51
0:12:51
 0:08:28
0:08:28
 0:10:44
0:10:44
 0:07:49
0:07:49
 0:10:04
0:10:04
 0:13:10
0:13:10
 0:09:19
0:09:19