filmov
tv
Isomorphism

Показать описание
What does it mean for two spaces to be isomorphic? In this video, I define the notion of isomorphism of vector spaces, and show that P2 and R3 are isomorphic.
Isomorphisms (Abstract Algebra)
What are Isomorphic Graphs? | Graph Isomorphism, Graph Theory
Isomorphism
Determine if two graphs are isomorphic and identify the isomorphism
What does isomorphic mean? What is an isomorphism?
Isomorphism Introduction
Isomorphism in Graph Theory in Hindi
Isomorphic Groups and Isomorphisms in Group Theory | Abstract Algebra
Discrete Math II - 10.3.2 Graph Isomorphisms
Chapter 6: Homomorphism and (first) isomorphism theorem | Essence of Group Theory
Is a linear transformation one to one? Onto? An isomorphism?
Functional Analysis 21 | Isomorphisms
Linear Algebra 8.3 Isomorphism
ISOMORPHISMS and BIPARTITE GRAPHS - DISCRETE MATHEMATICS
Isomorphism linear algebra Determine if linear transformation is an isomorphism
Isomorphism of Graphs with Examples - Graph Theory - Discrete Mathematics
Abstract Algebra - 6.1 Definition and Understanding of Isomorphisms
Isomorphic Graphs - Example 1 (Graph Theory)
Abstract Algebra | First Isomorphism Theorem for Groups
Abstract Algebra | Group Isomorphisms
Isomorphic Graphs
Visual Group Theory, Lecture 4.5: The isomorphism theorems
Circuit Isomorphism
Graph Theory: 10. Isomorphic and Non-Isomorphic Graphs
Комментарии
 0:05:04
0:05:04
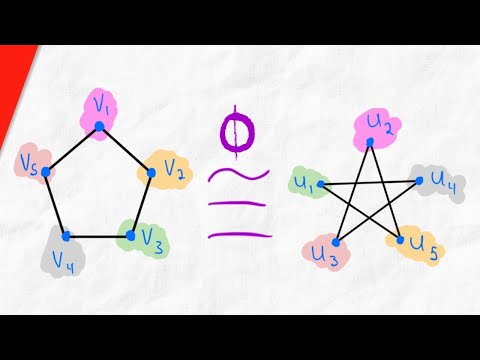 0:12:21
0:12:21
 0:12:51
0:12:51
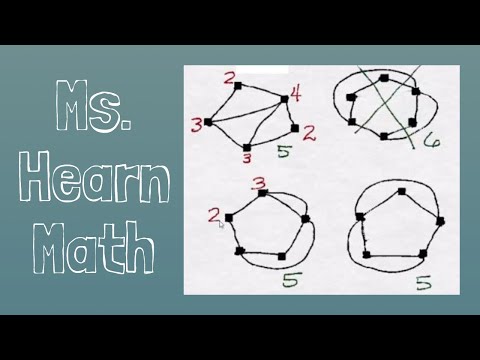 0:08:40
0:08:40
 0:12:46
0:12:46
 0:01:14
0:01:14
 0:08:35
0:08:35
 0:13:58
0:13:58
 0:13:14
0:13:14
 0:12:47
0:12:47
 0:06:09
0:06:09
 0:10:39
0:10:39
 0:16:37
0:16:37
 0:16:58
0:16:58
 0:06:29
0:06:29
 0:07:32
0:07:32
 0:20:41
0:20:41
 0:08:29
0:08:29
 0:15:35
0:15:35
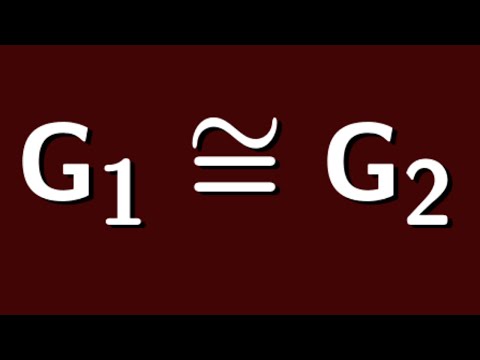 0:12:46
0:12:46
 0:06:59
0:06:59
 0:46:19
0:46:19
 0:00:15
0:00:15
 0:10:14
0:10:14