filmov
tv
An Exponential Log Equation #algebra
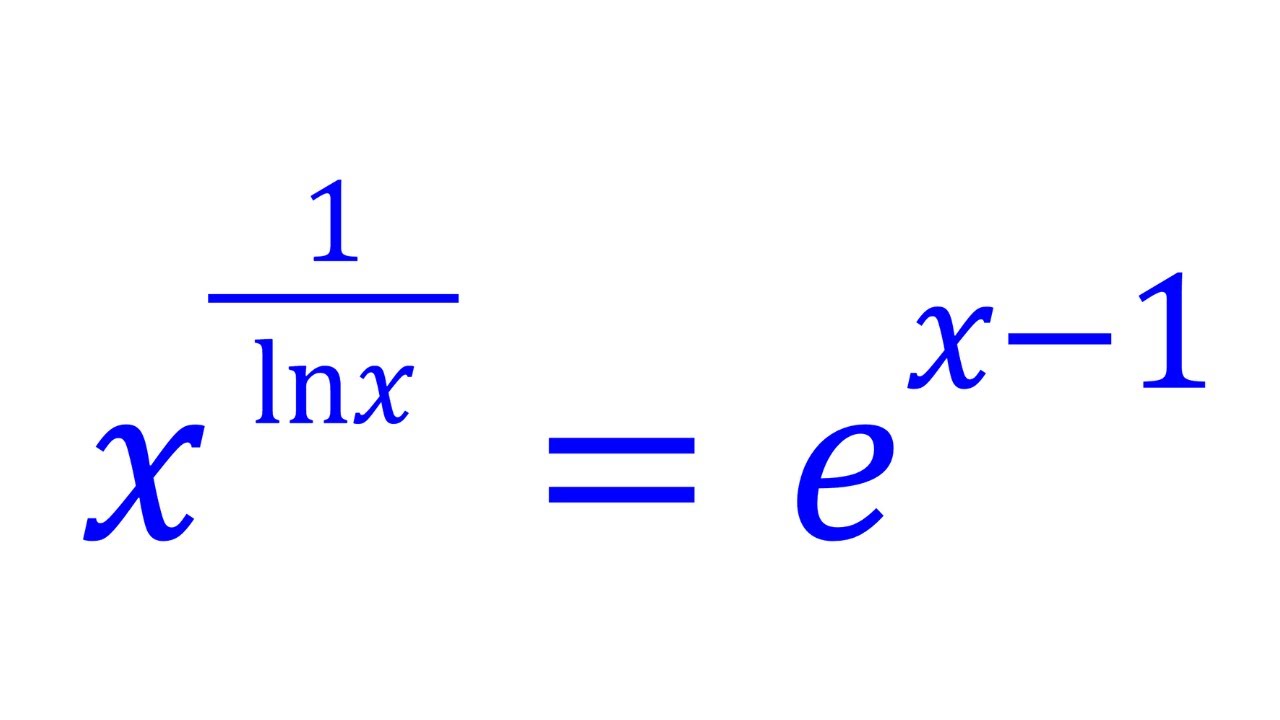
Показать описание
🤩 Hello everyone, I'm very excited to bring you a new channel (SyberMath Shorts).
Enjoy...and thank you for your support!!! 🧡🥰🎉🥳🧡
If you need to post a picture of your solution or idea:
#algebra #polynomials #exponentials #logs #trigonometry #calculus
via @YouTube @Apple @Desmos @NotabilityApp @googledocs @canva
PLAYLISTS 🎵 :
Enjoy...and thank you for your support!!! 🧡🥰🎉🥳🧡
If you need to post a picture of your solution or idea:
#algebra #polynomials #exponentials #logs #trigonometry #calculus
via @YouTube @Apple @Desmos @NotabilityApp @googledocs @canva
PLAYLISTS 🎵 :
Solving Exponential and Logarithmic Equations
Logarithmic Form to Exponential Form (Natural Log Edition) 🤯 #Shorts #algebra #math #education
Logarithms, Explained - Steve Kelly
Natural Logarithms
Exponential Form to Logarithmic Form #Shorts #algebra #math #maths #mathematics #lesson #howto
Exponential Logarithmic Equations
Logarithmic Form to Exponential Form 🤯 #Shorts #algebra #math #maths #mathematics #education #learn...
Solving Exponential Equations
Exponential Equations: Top Tips for Math Olympiad Competitors
Solving Logarithmic Equations
The Exponential Function e and The Natural Log ln
How to Graph Exponential Functions
Solving Exponential Equation
Exponential Equations - Algebra and Precalculus
Writing Logarithmic Equations In Exponential Form
Solving logarithmic equations | Exponential and logarithmic functions | Algebra II | Khan Academy
Solving exponential equation | Exponential and logarithmic functions | Algebra II | Khan Academy
Algebra 2 - Solving Exponential & Logarithmic Equations
Introduction to Logarithms (1 of 2: Definition)
Solving exponential equations by using the natural log
How to Write a Logarithmic Equation in Exponential Form an Example with a Fraction
Solving Exponential Equation
Solving exponential equation with logarithm | Logarithms | Algebra II | Khan Academy
Logs Everything You Need to Know
Комментарии
 0:07:08
0:07:08
 0:00:28
0:00:28
 0:03:34
0:03:34
 0:02:49
0:02:49
 0:00:22
0:00:22
 0:06:43
0:06:43
 0:00:14
0:00:14
 0:16:36
0:16:36
 0:05:27
0:05:27
 0:25:27
0:25:27
 0:10:16
0:10:16
 0:00:40
0:00:40
 0:00:56
0:00:56
 0:05:58
0:05:58
 0:03:07
0:03:07
 0:04:13
0:04:13
 0:05:12
0:05:12
 0:10:54
0:10:54
 0:07:53
0:07:53
 0:02:23
0:02:23
 0:00:22
0:00:22
 0:00:54
0:00:54
 0:02:51
0:02:51
 0:20:27
0:20:27