filmov
tv
A RIDICULOUSLY AWESOME INTEGRAL!!! real vs complex methods with @qncubed3

Показать описание
This video answers a question as old as time itself; is there an integral that has an absolutely gorgeous solution using both real and complex methods of integration?
Well here's that integral along with 2 wonderful solution developments with real and complex methods by me and qncubed3 respectively.
Well here's that integral along with 2 wonderful solution developments with real and complex methods by me and qncubed3 respectively.
A RIDICULOUSLY AWESOME INTEGRAL!!! real vs complex methods with @qncubed3
A ridiculously awesome integral with an epic result
A RIDICULOUSLY AWESOME integral from the quantum realm
A RIDICULOUSLY AWESOME LOG INTEGRAL!!!
A RIDICULOUSLY AWESOME FRACTIONAL TRIGONOMETRIC INTEGRAL!!!
Another ridiculously awesome integral with a beautiful result
A ridiculously awesome infinite power tower integral!!!
A RIDICULOUSLY AWESOME INTEGRAL: The best thing you are going to see this weekend!
DocuPanda and Make.com integration - automatically analyze every invoice
A RIDICULOUSLY AWESOME INTEGRAL: Ramanujan vs Maths 505
A RIDICULOUSLY AWESOME INTEGRAL!!! int ln(Gamma(x+1)) from 0 to 1
What is Integration? 3 Ways to Interpret Integrals
2 ridiculously awesome log integrals solved using contour integration
An awesome integral for friday night
The Bernoulli Integral is ridiculous
A RIDICULOUSLY AWESOME LOG INTEGRAL: Integral of (ln(x))^2/(x^2+1) from zero to infinity
Revisiting an awesome integral
An awesome generalized integral!
This epic integral is the best thing you'll see today!
A crazy yet perfect integral
This Will Be Your Favorite Integral
A gamma-digamma integral #calculus #gamma #advancedmaths #integral #integration #complexanalysis
Solving an awesome integral using Feynman's technique
Solving this awesome integral using one of the best substitutions you'll ever see!
Комментарии
 0:24:21
0:24:21
 0:13:43
0:13:43
 0:08:05
0:08:05
 0:08:20
0:08:20
 0:15:53
0:15:53
 0:14:11
0:14:11
 0:10:24
0:10:24
 0:26:20
0:26:20
 0:14:21
0:14:21
 0:18:23
0:18:23
 0:08:39
0:08:39
 0:10:55
0:10:55
 0:26:14
0:26:14
 0:09:51
0:09:51
 0:10:00
0:10:00
 0:10:16
0:10:16
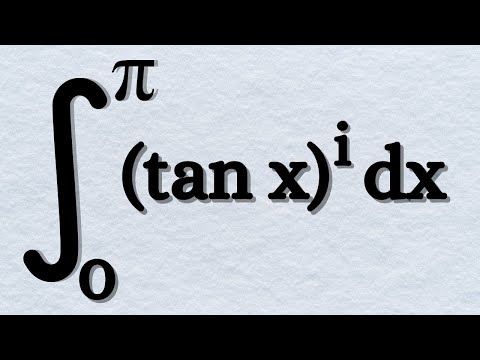 0:06:51
0:06:51
 0:08:23
0:08:23
 0:25:35
0:25:35
 0:12:24
0:12:24
 0:04:29
0:04:29
 0:00:58
0:00:58
 0:09:02
0:09:02
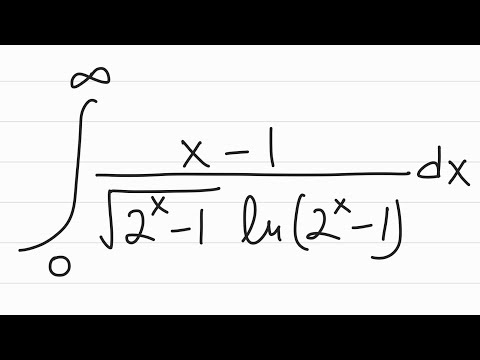 0:11:37
0:11:37