filmov
tv
This Will Be Your Favorite Integral
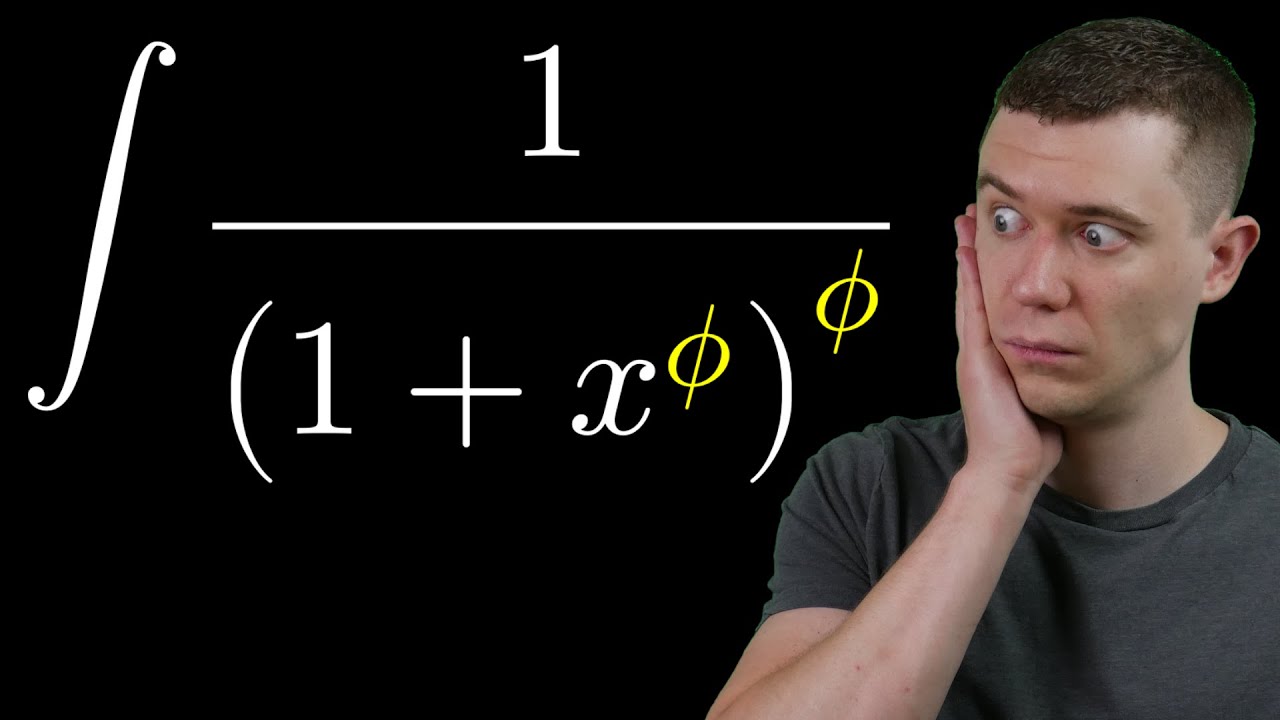
Показать описание
The golden ratio is a pretty famous math inequality. BUT have you heard of (what I call) the Golden Integral?
This Golden Ratio Integral integrates to a pretty remarkable result!
🙏Support me by becoming a channel member!
Disclaimer: This video is for entertainment purposes only and should not be considered academic. Though all information is provided in good faith, no warranty of any kind, expressed or implied, is made with regards to the accuracy, validity, reliability, consistency, adequacy, or completeness of this information.
#math #brithemathguy #goldenratio
This Golden Ratio Integral integrates to a pretty remarkable result!
🙏Support me by becoming a channel member!
Disclaimer: This video is for entertainment purposes only and should not be considered academic. Though all information is provided in good faith, no warranty of any kind, expressed or implied, is made with regards to the accuracy, validity, reliability, consistency, adequacy, or completeness of this information.
#math #brithemathguy #goldenratio
'Your life will be based by your favorite song' ||GC meme||
This Will Be Your Favorite Simple Problem
This will be your new FAVORITE integral!
I will sing your favorite song #gachatrend
Everyone will teleport to their favorite game ||gacha club|| ||meme|| 🎮🌌❤️✨
Your favorite song will become your life ✨ 💕 || Ppg 🌈 || Trend
😿[]Your favorite song will be your life!😿[]Gacha Life Meme[]Fw!!Og Concept
What Your Favorite Will Wood Song Says About You
Choose Your Favorite Superhero: Who Will You Be?
🎶your favorite song will become your life📣_____🌠old meme/trend?🌠_____Part 1🙂[I'm blue (La ba de...
Your favorite song will become your life. 💖 trend (FNAF)
Your favorite song will become your life meme/fnaf
This Will Be Your Favorite Shape
' your favorite song will become your life ' | bnha/mha | gacha meme/trend
This Steak Sandwich will be Your Favorite | Relaxing Cooking in Nature ASMR
you will be teleporting to your favorite game! ||gacha life||
This Will Be Your NEW Favorite Pasta Recipe, GUARANTEED!
Attention Coffee Lovers: This Will Become Your Favorite Cake!
'𝗬𝗼𝘂𝗿 𝗳𝗮𝘃𝗼𝗿𝗶𝘁𝗲 𝘀𝗼𝗻𝗴 𝘄𝗶𝗹𝗹 𝗯𝗲𝗰𝗼𝗺𝗲 𝘆𝗼𝘂𝗿 𝗹𝗶𝗳𝗲'..-// Mha // Deku Angst // DekuTodo // 🦋‼️...
Your favorite song will become your life // BakuDeku/DekuBaku // Original Concept //
Your Favorite Song will Become Your Life || Meme || MLB || AU || Trend || Gacha Club
pov: You will be teleported to your favorite game! #trend #edit #gacha #gachalife #gacha
🎶[] Your Favorite Song Will Become your Life [] MeMe [] Gacha Life []🎶
This Will Be Your Favorite MEAT #shorts #foodlover #comedy
Комментарии
 0:00:16
0:00:16
 0:03:03
0:03:03
 0:11:14
0:11:14
 0:00:24
0:00:24
 0:00:14
0:00:14
 0:00:33
0:00:33
![😿[]Your favorite song](https://i.ytimg.com/vi/XuFY7nywsak/hqdefault.jpg) 0:00:14
0:00:14
 0:00:59
0:00:59
 0:00:35
0:00:35
 0:00:38
0:00:38
 0:00:19
0:00:19
 0:00:28
0:00:28
 0:06:32
0:06:32
 0:00:27
0:00:27
 0:13:26
0:13:26
 0:00:16
0:00:16
 0:09:58
0:09:58
 0:03:06
0:03:06
 0:00:47
0:00:47
 0:01:53
0:01:53
 0:00:40
0:00:40
 0:00:23
0:00:23
![🎶[] Your Favorite](https://i.ytimg.com/vi/H6-vjlAIebU/hqdefault.jpg) 0:00:29
0:00:29
 0:00:07
0:00:07