filmov
tv
A crazy yet perfect integral
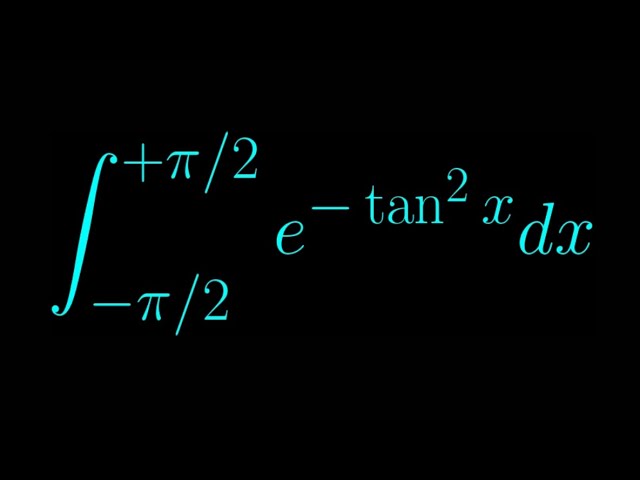
Показать описание
Here's another awesome integral with a beautiful solution development using Feynman's trick and the error function.
A crazy yet perfect integral
Math Integration Timelapse | Real-life Application of Calculus #math #maths #justicethetutor
This famous integral is perfect for Feynman's integration technique
Check out this crazy integral trick!
A Top G Integral
A RIDICULOUSLY AWESOME INTEGRAL WITH A BEAUTIFUL RESULT!!!
A gamma-digamma integral #calculus #gamma #advancedmaths #integral #integration #complexanalysis
A RIDICULOUSLY AWESOME INTEGRAL: solution using Feynman's technique
So much to learn/review in one integral!!!
The INSANE floor integral from the 2022 MIT integration bee finals
🔥 Only 1% Can Solve This INSANE Integral! 🤯 | 200 IQ Math Challenge #JEE #Calculus #maths #jeemains...
An interesting generalised integration result: int 1/(1+x^s)^s from 0 to infinity
How to Answer Any Question on a Test
An e^xtreme integral!
Derivative of a Function Defined as an Integral, but on Steroids
You'll love this embedded integral
a quick antiderivative problem from the MIT integration bee finals (2022)
Beautiful Integral, exponential pyramid
Immigrant in Norway? What are the challenges? Job? Integration? All on my page! #norway #immigrants
Watch as Inmate ESCAPES COURTHOUSE UNNOTICED | Court Cam | A&E #shorts
MIT Integration Bee 2011 #11
Full auto Nerf Stryfe x Centurion integration (W.I.P)
A weird integral - 2019 FAMAT Calculus Individual #25
Our sensory swing has become our go-to tool for sensory integration and stimulation! #sensoryplay
Комментарии
 0:12:24
0:12:24
 0:00:09
0:00:09
 0:10:57
0:10:57
 0:07:57
0:07:57
 0:09:25
0:09:25
 0:09:56
0:09:56
 0:00:58
0:00:58
 0:12:35
0:12:35
 0:36:39
0:36:39
 0:15:37
0:15:37
 0:01:13
0:01:13
 0:13:56
0:13:56
 0:00:27
0:00:27
 0:08:48
0:08:48
 0:04:41
0:04:41
 0:05:47
0:05:47
 0:04:19
0:04:19
 0:02:42
0:02:42
 0:00:16
0:00:16
 0:01:00
0:01:00
 0:03:44
0:03:44
 0:00:05
0:00:05
 0:13:14
0:13:14
 0:00:19
0:00:19