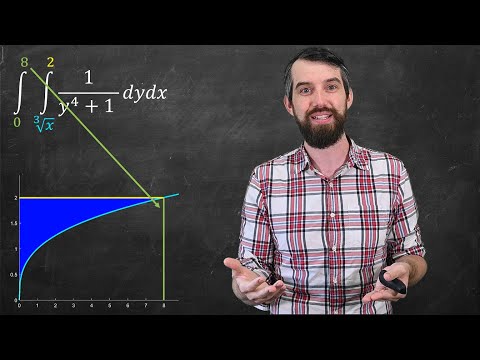
What is Integration? 3 Ways to Interpret Integrals

Integrals Explained! This video explains 3 ways to understand and interpret integrals in calculus. Two of these ways are commonly taught in school. But one way is often left behind but really unlocks real world problem solving! These conceptions of integration are then applied to real world problems.

Math The World is dedicated to bringing real world math problems into the classroom and answering the age old question “when will I ever use this?”

We use unique algebra context topics, geometry context topics, trigonometry context topics, and calculus context topics. We go beyond context problems and use a technique called mathematical modeling to find solutions to real world questions and real world problems. These videos are great for students who plan to enter technical fields that require real world problem solving, and can be a great resource for teachers looking for ways to bring real world contexts into their classroom.

Created by Doug Corey

Script: Doug Corey and Jennifer Canizales
Audio: Doug Corey
Animation: Jennifer Canizales
Music: Tech House

© 2023 BYU

[Tubeytime]

The claim of this video was not clickbait! That absolutely helped me understand it better and it should be the default way of teaching this subject.

[maxlin]

As a senior in mechanical engineering, I can attest to the importance of this. When you’re looking at heat flow or force concentration, a lot of the methods and equations are derived from this idea of adding up many tiny bits after applying some function to them. Good work here!

[hcn]

I really understood integration after taking Physics, it helped me think better of it as adding up tiny amounts of stuff

[blacklistnr]

I cannot emphasize enough how much the idea at 3:35 has been useful to me so far.
The fact that any (usual) function looks like a line if you zoom in enough opens so many doors in limits, numerical approximations & computing, not to mention linear algebra.
It's crazy how teachers gloss over this

[rarebeeph]

This is absolutely how I think of integration. Whenever people try to say they'll never use calculus, or that it's too complex, I always tell them that calculus is the math of rates and totals, which, I think, are both very fundamental concepts for interacting with the world.
And they're both very nicely captured, as you showed, by discrete problems, which are much simpler to conceptualize. The derivative corresponds to the difference between consecutive elements of a sequence, and the integral corresponds to the sum of consecutive elements of a sequence. By expanding out the terms of a sum of differences, you find that tons of things cancel, yielding the analog for the fundamental theorem of calculus. They even have a close analog to the product rule, and therefore, integration/summation by parts. I think it's often a missed opportunity in math classes that they don't clearly make these connections. Great video!

[jobobminer]

Jokes in you. I didn't learn it at all

[Burnrate]

Just so you know, at 1:40, bows bend when you pull the string back. You aren't stretching the string. Also, the reason the force curve flattens and gets lower at the top is because of the additional mechanical parts of a compound bow that are designed to make it easier to hold at a full draw.

[foxglovelove]

I always enjoy the moment I tell people about the integral symbol just being an elongated "S" because it's a sum, and just watching the light bulb turn on in real time. Very satisfying

[Swanicorn]

In my school we were asked to draw different standard shapes with provided dimensions like a square, triangle, circle, hexagon etc on a graph paper. Then were asked to add up the tiny 1mm squares to find the area. We were then taught the formula and we were also explained how that formula can be derived using what we were doing on the graph paper: adding and multiplying many small things. Later we did that to volumes as well and finally 3D vectors in graduation level math, electromagnetics etc. It is surprising to me how so many comments are saying they didn't do this or their teacher glossed over this.

[camicus-]

I definitely found this was one of the biggest differences between calculus in maths class vs later on in engineering.
With questions like "is dy/dx a fraction?", a maths teacher would say no and (understandably) focus more on rigour and strict definitions. Meanwhile, engineering professors would be much more cowboyish and would freely treat dy and dx as any other variable. Obviously mathematical rigour is necessary, but sometimes focusing too much on it can obfuscate the core ideas and distance people from a more intuitive approach

[Puzomor]

I always felt that to understand a tool or a solution, it was very important to understand the original problem and the initial solution that gave rise to the refined solution.

[logers]

I was just wondering why my modern physics lab had us work out the sum of a bunch of discrete averages instead of just integrating some given wavefunction, now I get what they were trying to do. Great video.

[ciroguerra-lara]

My physical chemistry teacher, with regards to classic thermodynamics and steady state transport phenomena, used the concept of a "physical integral". It is basically what you described.

[melineeluna]

Footpound sounds way more like a Pokémon move than a unit of force

[SteinGauslaaStrindhaug]

This is a major reason I feel like I understood and learned so much more maths in the physics class than in the maths class... Derivation and integration is so much easier in physics; it means something: finding velocity from distance, distance from velocity, acceleration from velocity, and jerk, snap, crackle, pop if you go on. And you "calculate" the integral simply by summing up the slices under the curve, and find the derivative by examining the slope at every point; and since it's physics and the curve is not a mathematical construction usually but a measurement in the first place you don't have to fiddle with the sumbolic derivation/integration since there is no actual alternative than to estimate/interpolate the values from the curve/plot itself.

Also my maths teacher was terrible, and had absolutely no comprehension of how anyone could not understand maths in the same way as him immediately; so I eventually switched from the physics/engineering oriented maths class to the statistics oriented class to get another teacher.

I think I do remember the symbolic way to do it; but it was boring the way it was done in maths class because it was completely divorced from any practical application, and because the maths teacher was an uninspired idiot; he didn't even connect it with anything interesting within maths either. It was purely mindless busywork with no insights or application or fun at all with him.

[loganhagendoorn]

This is 100% true, and something I like to tell all of my friends that are struggling in calculus. When I was in AP Physics 1, I had heard that moment of inertia formulas could be calculated using integrals, and because I had no idea that an integral was anything more than the area under a curve, I couldn't conceptualize this. Eventually, I went on a long derivation trying to find the formula of the moment of inertia of a cylinder using the summation form of an integral (limit as the upper bound approaches infinity), and I finally made the connection.

[xavidoor]

The tiny-bit sum conception is especially useful when you start working with surface and volume integrals.

[carlosoliveros]

I wish I could watch your explanation 18 years ago. This is so delightful to see.

[sebastianfia]

Great vid, but doing physics using feet and lbs should be illegal

[aatifhussain]

If you watch this video in reverse you will learn differentiation!