Olympiad Geometry Problem #86: IMO Shortlist 2019 G2

preview_player
Показать описание
Here is a fascinating problem that was recently released as one of the candidate problems for the 2019 International Math Olympiad (although it didn't end up making it on the exam). The solution I give is not the simplest, but is fairly insightful in my opinion. Enjoy! Links below.
  1. Michael Greenberg
Рекомендации по теме
Olympiad Geometry Problem 0:14:46

Olympiad Geometry Problem #86: IMO Shortlist 2019 G2

Olympiad Geometry Problem 0:21:37

Olympiad Geometry Problem #84: IMO Shortlist 2012 G6

Problem 86. Circles 0:10:25

Problem 86. Circles and Lines

Olympiad Geometry Problem 0:10:58

Olympiad Geometry Problem #37: IMO 2018 #1

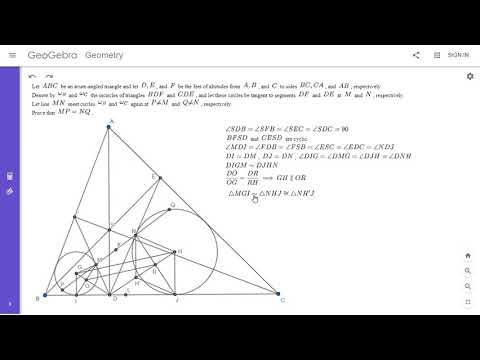
Olympiad Geometry Problem 0:14:05

Olympiad Geometry Problem #87: Altitudes, Circumcircles, Parallel

Olympiad Geometry Problem 0:12:25

Olympiad Geometry Problem #64: IMO Shortlist 2017 G1

HOW CHINESE STUDENTS 0:00:23

HOW CHINESE STUDENTS SO FAST IN SOLVING MATH OVER AMERICAN STUDENTS

IMO Shortlist 2013 0:07:23

IMO Shortlist 2013 - N3: This one is cool

Only for a 0:00:20

Only for a Genius! Connect 1 to 1, 2 to 2 & 3 to 3 without crossing the lines! #math #youtube

Olympiad Geometry Problem 0:10:33

Olympiad Geometry Problem #35: Angle Bisector, Perpendiculars, Tangency

Olympiad Geometry Problem 0:09:32

Olympiad Geometry Problem #97: Incircle, Tangency Points, Concurrence

The Esteemed solution 0:06:56

The Esteemed solution | Olympiad Geometry Math Question 2|INMO shortlist|#olympiad #olympiadproblem

IMO ShortList 2019 0:06:36

IMO ShortList 2019 - Problem G1: A intro SL geometry problem

If A_1, A_2 0:01:00

If A_1, A_2 be area of circles with radii √86 a^3 b^3 & a^2 b^2, find the maximum value of A_1/A...

IMO 2007 Geometry 0:24:54

IMO 2007 Geometry Problem |Method to solve FE-Fixed pt | Learn Hatke Spcl | Maths 101| Rahul Rohilla

A geometry I 0:33:54

A geometry I proposed for the BMO 2017 - BMO SL G5

International Math Olympiad, 0:06:11

International Math Olympiad, IMO 2021, Shortlisted Problem, A2

IMO 2019 0:11:35

IMO 2019 P1

Olympiad Geometry Problem 0:11:22

Olympiad Geometry Problem #70: Cyclic Quad, Equal Segements, Perpendicuar

Solving the famous 0:11:06

Solving the famous IMO 2010 Problem 1! (Substitution Strategy)

LIII International Mathematical 0:09:50

LIII International Mathematical Olympiad 2012, Mar del plata - Argentina: problema 5 (English ver.)

Nice Math Equation| 0:04:15

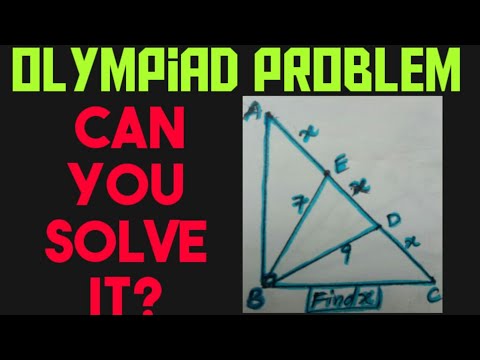
Nice Math Equation| Math Olympiad Questions| Find the Unknown Term|

IIT Bombay Lecture 0:00:12

IIT Bombay Lecture Hall | IIT Bombay Motivation | #shorts #ytshorts #iit

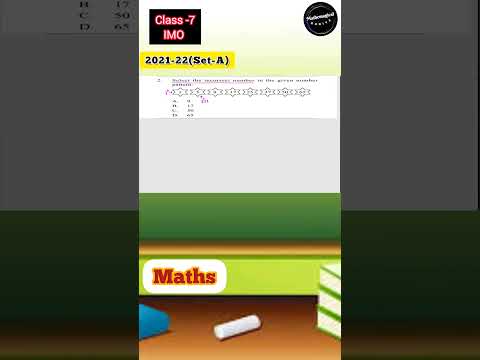
Class-7 IMO 2021-22|Logical 0:00:40

Class-7 IMO 2021-22|Logical Reasoning| #maths #imo #olympiad #cbse #class7 @mathemagicalduniya

Комментарии
Автор

truely amazing! thanks for uploading beautiful solution.

김동욱-wtz
Автор

Nice solution👌🏻
I solved the problem in the same way but I did the step, showing that RO and KL are perpendicular, in another (I think shorter) way. Because K, O, L and R are the Midpoints of the quadrilateral IJNM, KOLR has to be a parallelogram. Because of DJ=DN, DM=DI and <JDM=<NDI, we know, JDM~NDI an therefor JM=NI. Thus KOLR is a Rhombus and so the diagonals KL and RO are perpendicular.

germanyop
Автор

When the gilding principle is used I still don't get what is the definition of oriented the same way.

helo