Olympiad Geometry Problem #64: IMO Shortlist 2017 G1

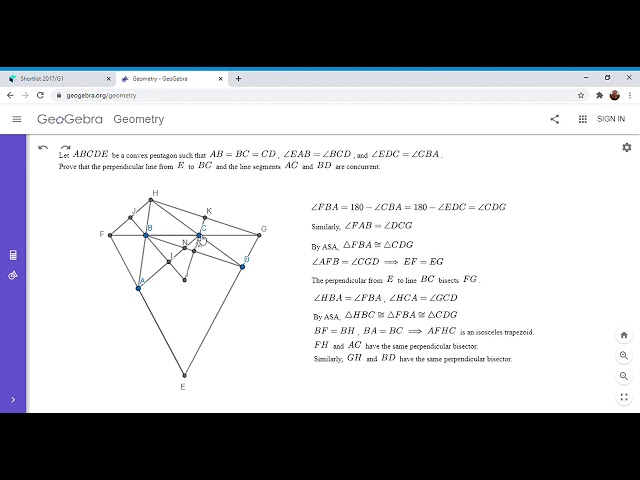
preview_player
Показать описание
Here is a very entertaining problem from the 2017 IMO Shortlist, with a very specific starting configuration. Although it was the first of the geometry problems on the shortlist, I did not find it to be that easy. Enjoy! Link below.
  1. Michael Greenberg
Рекомендации по теме
Olympiad Geometry Problem 0:12:25

Olympiad Geometry Problem #64: IMO Shortlist 2017 G1

A beautiful international 0:01:00

A beautiful international math olympiad problem

Olympiad Geometry Problem 0:11:20

Olympiad Geometry Problem #65: IM Lemma

Olympiad Geometry Problem 0:13:34

Olympiad Geometry Problem #73: IMO Shortlist 2005 G6

Olympiad Geometry Problem 0:20:24

Olympiad Geometry Problem #32: IMO 2019 #6

64th International Mathematical 0:00:57

64th International Mathematical Olympiad (IMO) 2023, Japan Logo

Olympiad Geometry Problem 0:12:11

Olympiad Geometry Problem #38: IMO Shortlist 2012 G4

IMO 2023 Day 0:39:05

IMO 2023 Day 1 solutions and discussion

Germany | Olympiad 0:02:31

Germany | Olympiad Mathematics | Can You Solve This?

Olympiad Geometry Problem 0:16:24

Olympiad Geometry Problem #72: Tangent, Isoceles Triangles, Collinear

A Nice Olympiad 0:00:52

A Nice Olympiad Exponential Multiplication Problem #short #olympiad #mathematics #maths #exponents

Sweden Olympiad Geometry 0:11:59

Sweden Olympiad Geometry Problem I OLYMPIAD I SAT I MCAT I Xth I GRE I Pre-Math I NSO | IMO | SOF

IMO 2000 Geometry 0:14:34

IMO 2000 Geometry | INMO Question of the Day | INMO 2022-23 | Chetan Garg | VOS

A Nice Math 0:02:34

A Nice Math Olympiad Exponential Equation 3^x = X^9

Who is the 0:00:49

Who is the largest? (Magical Inequalities)

China Math Olympiad 0:07:13

China Math Olympiad 2020 Day 2 Problem 4 solution

Mexico - A 0:08:36

Mexico - A Nice Math Olympiad Exponential Problem

When mathematicians get 0:00:37

When mathematicians get bored (ep1)

Olympiad Geometry Problem 0:14:46

Olympiad Geometry Problem #86: IMO Shortlist 2019 G2

Olympiad Geometry Problem 0:13:51

Olympiad Geometry Problem #68: Orthocenters, Midpoint, Cyclic Quad

Olympiad Geometry Problem 0:13:29

Olympiad Geometry Problem #57: Altitudes, Midpoint, Circumcircle

Canadian Math Olympiad 0:01:33

Canadian Math Olympiad Question | Find the area of shaded region.

Indian vs Japanese 0:00:13

Indian vs Japanese Maths 🔥| Vedic Maths Trick for Fast Calculation | Speed Maths #trending #shorts...

First International Maths 0:07:50

First International Maths Olympiad Question | IMO 1959 | Proof by Absurdity or Contradiction

Комментарии
Автор

Hey Michael! Thanks a lot on all those amazing geo videos! You are the one that built up my geo skills and now I am confident about solving USAMO Problems.

helo
Автор

Hey Michael! I have always loved mathematics as a kid and have been pretty good at it, but for some reason i could never get my head around geometry. For olympiad problems, geometry became a gray, terrifying area. But ever since i found you channel, i am absolutely LOVING geometry!
I have watched half of your playlist while practicing problems.
Keep up the AMAZING work!!

❤️ Love from India Sir

gamedepths
Автор

Oh god you are such a genius I wish I had your talant

zukazuka
Автор

Amazing solution!, this was exactly the same as my initial approach, but I failed to see that I was the circumcenter of FHG so I couldn't finish the problem through this way and had to take the pappus' route :(

prithujsarkar