filmov
tv
Olympiad Geometry Problem #97: Incircle, Tangency Points, Concurrence

Показать описание
Here is an enlightening problem with a simple configuration but which is still tricky to solve. It was posted on the Art of Problem Solving Forum last year, but I don't know the original source. Enjoy! Link below.
Olympiad Geometry Problem #97: Incircle, Tangency Points, Concurrence
Olympiad Geometry Problem #98: Circumcenter, Midpoints, Equal Angle
Olympiad Geometry Problem #50: Incenter, Midpoint, Parallel
Olympiad Geometry Problem #29: Incenter, Perpendicular, Equal Angles
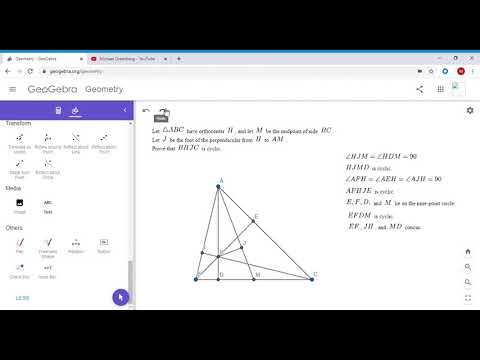
Olympiad Geometry Problem #5: H-M Theorem
Olympiad Geometry Problem #46: Circumcenter, Parallel, Orthocenter
Olympiad Geometry Problem #88: IMO Shortlist 2019 G6
Olympiad Geometry Problem #84: IMO Shortlist 2012 G6
Olympiad Geometry Problem #55: Projective Geometry Part 2
UKMT olympiad training | Maclaurin 2008 Q4 | Geometry
Olympiad Tricky Geometry Question | Singapore Secondary School Mathematical Olympiad .
Ep37 - Tricky geometry sums, Olympiad made easy, learn Mathematics
The Complete Orthocentre Configuration: A path to a CELEBRATED circle!
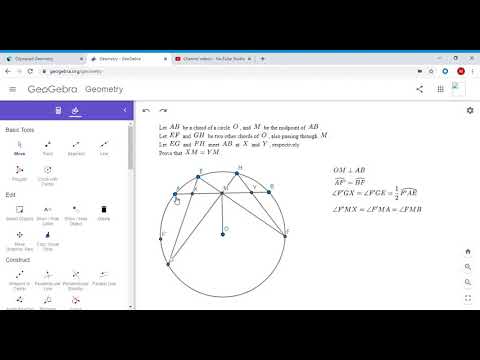
Olympiad Geometry Problem #4: Butterfly Theorem
Olympiad Geometry Problem #34: IMO Shortlist 2002 G7
LIVESTREAM GEO #96A: We Added a Lot of New Points to the Diagram for the Second Problem!
Olympiad Geometry Problem #51: Pascal's Theorem
Albert Einstein doing physics | very rare video footage #shorts
A tricky Geometry from the 2013 Balkan Math Olympiad BMO 2013 - P1
Math Olympiad: A Problem a Day (January 29th, 2019)
Olympiads: Geometry (1)
1996 IMO Problem #2 (Projective Geometry)
LIVESTREAM GEO #44A: One of the Hardest Problems Solved on Livestream!
Olympiad Math || Can You Solve This Equation||
Комментарии
 0:09:32
0:09:32
 0:09:30
0:09:30
 0:13:43
0:13:43
 0:10:30
0:10:30
 0:12:01
0:12:01
 0:09:22
0:09:22
 0:14:51
0:14:51
 0:21:37
0:21:37
 0:11:04
0:11:04
 0:03:20
0:03:20
 0:02:12
0:02:12
 0:04:55
0:04:55
 0:15:12
0:15:12
 0:13:29
0:13:29
 0:17:07
0:17:07
 1:27:02
1:27:02
 0:06:36
0:06:36
 0:00:13
0:00:13
 0:21:31
0:21:31
 0:03:18
0:03:18
 0:03:51
0:03:51
 0:12:41
0:12:41
 1:47:48
1:47:48
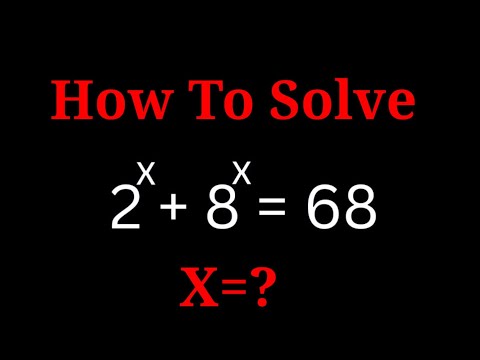 0:07:11
0:07:11