filmov
tv
Solve the Exponential Equation | (6 - x)^(x^2 + 7x + 12) = 1 | Quadratic Equation

Показать описание
Solve the Exponential Equation (6 - x)^(x^2+7x+12)=1
Solution of this equation involve three different cases
case 1: 6 - x = 1
case 2: 6 - x = -1 when x^2+7x+12 = even number
case 3: x^2+7x+12 = 0 when 6 - x ≠ 0
Solution of this equation involve three different cases
case 1: 6 - x = 1
case 2: 6 - x = -1 when x^2+7x+12 = even number
case 3: x^2+7x+12 = 0 when 6 - x ≠ 0
Solving Exponential Equations
Exponential Equations - Algebra and Precalculus
Solving Exponential Equation
Solving Exponential Equation
Solving Exponential Equations
Solve an exponential equation by taking log of both sides & approximating the value
Solving an exponential equation
Exponential Equation Grade 10
A Nice Math Olympiad Question | Can You Solve this ? | Exponential Problem |
Solving exponential equations using exponent properties | High School Math | Khan Academy
How do you solve an exponential equation with e as the base
How to Solve Exponential Equations using Logarithms - No Common Base Present
Solving Exponential Equations | How to Solve Exponential Equations | General Mathematics
Solving Exponential and Logarithmic Equations
Exam Exponential Equations Grade 9
Solving exponential equations with different bases
Solving Exponential Equations with Common Bases | Algebra
Solving exponential equation | Exponential and logarithmic functions | Algebra II | Khan Academy
Solving Exponential Equations
Learn How to Solve Exponential Equations Using Two Different Methods | Step-by-Step Tutorial
08 - Solving Exponential Equations - Part 1 - Solve for the Exponent
How to solve an exponential equation with two different bases
Solving an exponential equation with different bases
Solving Exponential equations
Комментарии
 0:16:36
0:16:36
 0:05:58
0:05:58
 0:00:56
0:00:56
 0:02:56
0:02:56
 0:01:46
0:01:46
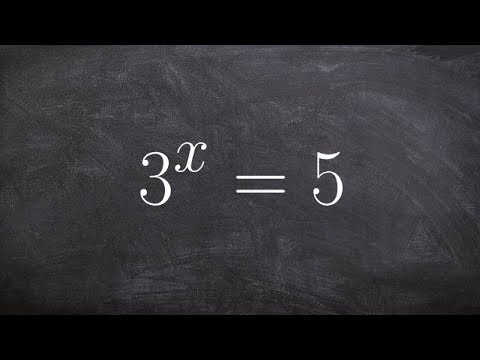 0:03:23
0:03:23
 0:03:14
0:03:14
 0:01:39
0:01:39
 0:08:53
0:08:53
 0:04:56
0:04:56
 0:02:47
0:02:47
 0:05:47
0:05:47
 0:11:33
0:11:33
 0:07:08
0:07:08
 0:04:34
0:04:34
 0:04:41
0:04:41
 0:00:55
0:00:55
 0:05:12
0:05:12
 0:20:04
0:20:04
 0:12:15
0:12:15
 0:18:28
0:18:28
 0:05:11
0:05:11
 0:03:01
0:03:01
 0:01:52
0:01:52