Discuss Collision Theory of Rate of reaction | Chemical Kinetics | Physical Chemistry

Показать описание

According to collision theory, two molecules must collide before they react. Of course, the collision is not the only reason for the reaction to take place. The rate of reaction is much different from the rate of collision. The colliding molecules must also possess sufficient energy for activation. It means out of all collisions only those collisions are useful which involve activated molecules.

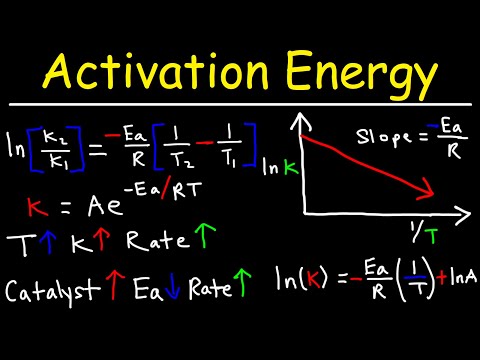
The van't Hoff equation relates the change in the equilibrium constant left( { K }_{ eq } right) of a chemical reaction to the change in temperature left( T right) . This Van't Hoff's relation is: boxed { frac { dleft( ln { K } right) }{ dT } = frac { triangle E }{ R{ T }^{ 2 } } } ... (1) where triangle E is energy of activation, R is gas constant, T is temperature and K is the equilibrium constant for the reaction. Consider a reversible reaction, A + B begin{matrix} { k }_{ 1 } Longleftrightarrow { k }_{ 2 } end{matrix} C + D Equilibrium constant K can be taken as frac { { k }_{ 1 } }{ { k }_{ 2 } } , where { k }_{ 1 } and { k }_{ 2 } are the velocity constants for the forward and back ward reactions. If { E }_{ 1 } and { E }_{ 2 } are the activation energies of the reactant and the product, then substituting these values in the above Van't Hoff's equation we get, frac { dleft( ln { frac { { k }_{ 1 } }{ { k }_{ 2 } } } right) }{ dT } = frac { left( { E }_{ 1 } - { E }_{ 2 } right) }{ R{ T }^{ 2 } } frac { dleft( ln { { k }_{ 1 } } - ln { { k }_{ 2 } } right) }{ dT } = frac { left( { E }_{ 1 } - { E }_{ 2 } right) }{ R{ T }^{ 2 } } frac { dleft( ln { { k }_{ 1 } } right) }{ dT } - frac { dleft( ln { { k }_{ 2 } } right) }{ dT } = frac { { E }_{ 1 } }{ R{ T }^{ 2 } } - frac { { E }_{ 2 } }{ R{ T }^{ 2 } } ... (2) This equation can be written in two parts as follows: frac { dleft( ln { { k }_{ 1 } } right) }{ dT } = frac { { E }_{ 1 } }{ R{ T }^{ 2 } } ... (3) frac { dleft( ln { { k }_{ 2 } } right) }{ dT } = frac { { E }_{ 2 } }{ R{ T }^{ 2 } } ... (4) or in general, frac { dleft( ln { k } right) }{ dT } = frac { E }{ R{ T }^{ 2 } } ... (5) on rearranging we can write, dleft( ln { k } right) = frac { E }{ R } frac { dT }{ { T }^{ 2 } } This expression on integration gives, int { dleft( ln { k } right) } = frac { E }{ R } int { frac { 1 }{ { T }^{ 2 } } dT } ln { k } = frac { E }{ R } left( frac { -1 }{ T } right) + I where I is the constant of integration ln { k } = I + left( -frac { E }{ RT } right) on taking antilog of exponential we get, k = { e }^{ left[ I + left( -frac { E }{ RT } right) right] } k = { e }^{ left[ I right] } times { e }^{ left( sfrac { -E }{ RT } right) } boxed { k = A{ e }^{ sfrac { -E }{ RT } } } ... (7) Where { e }^{ left[ I right] } = A is another constant known as frequency factor. Equation (7) is Arrhenius equation. Arrhenius gave an equation to study the effect of temperature on rate of reaction.

Secondly, the increase in reaction rate with temperature is due to increase in number of collisions. This effect can be explained on the basis of activation theory of Arrhenius.

Qualitatively, the collision theory quite satisfactorily explains the four factors which influence the reaction rates.
1. The rate of reaction depends on the nature of reactants, because the energy of activation differs from one reaction to another.
2. The rate of reaction depends on the concentration of reactants because the number of collisions increases as the concentration is increased.
3. The rate of reaction depends on the temperature, because an increase of temperature increases the number of collisions and thus the rate of reaction increases.
4. The rate of reaction depends on the presence of catalyst, because in presence of catalyst the collisions are made more effective.

Numerical: The molecular diameter of { O }_{ 2 } and { H }_{ 2 } gases are 3.39A° and 2.47A°. When one gram of { O }_{ 2 } and 0.1 gram of { H }_{ 2 } are mixed in one { dm }^{ 3 } flask at 300K, what will be the number of collisions in { m }^{ -3 }{ s }^{ -1 }? (Avogadro constant = 6.023 times { 10 }^{ 23 } { mol }^{ -1 }) Solution: Given That, Molecular Wt of { O }_{ 2 } = 32 because 32 gm of { O }_{ 2 } contains 6.023 times { 10 }^{ 23 } molecules. therefore 1 gm of { O }_{ 2 } will contain frac { 6.023 times { 10 }^{ 23 } times 1 }{ 32 } molecules. = 1.88 times { 10 }^{ 22 }