filmov
tv
Learn how to solve a quadratic by completing the square with fraction
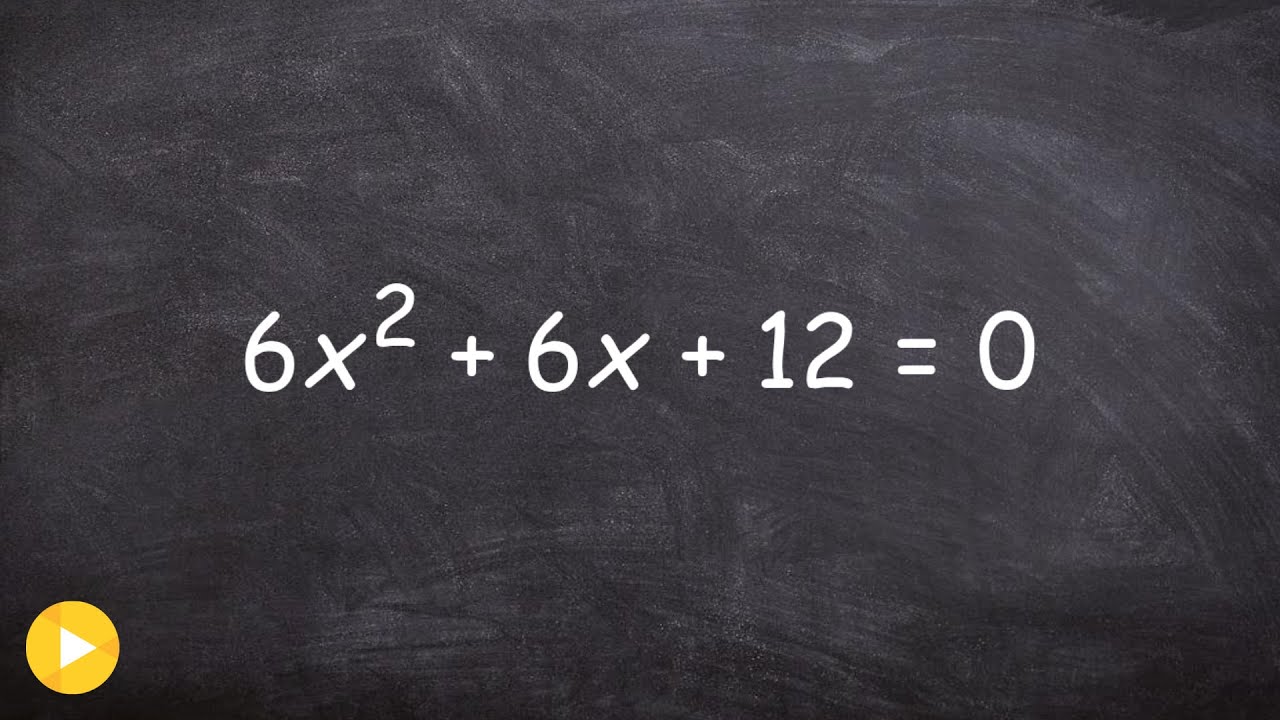
Показать описание
👉 Learn how to solve quadratic equations by completing the square. When solving a quadratic equation by completing the square, we first take the constant term to the other side of the equation and create a perfect square trinomial with the quadratic term and the linear term. If the coefficient of the quadratic term is not 1, we factor out the coefficient before creating the perfect square trinomial.
The perfect square trinomial is created by adding to both sides of the equation, the square of half the coefficient of the linear term (the term whose variable is not squared). Note that you must account for the factored out value when adding the square of half the linear term to the other side of the equation. Then the perfect square trinomial is evaluated and then we solve for the variable to get the solution(s) to the quadratic equation.
Timestamps:
0:00 Intro
0:40 Start of Problem
Corrections:
9:51 I made a mistake, -21/2 multiplied with 1/6 is -21/12. Final answer: -1/2 plus/minus \sqrt(21/12i)
Organized Videos:
✅How to Solve a Quadratic by Completing the Square
✅Solve a Quadratic by Completing the Square | Fractions
✅Solve a Quadratic by Completing the Square | -x^2+bx+c
✅Solve a Quadratic by Completing the Square | 2x^2+bx+c
✅Solve a Quadratic by Completing the Square | ax^2+bx+c
✅Solve a Quadratic by Completing the Square | x^2+bx+c
✅Solve a Quadratic by Completing the Square | Learn About
Connect with me:
#Solvequadratics #completethesquare #brianmclogan
The perfect square trinomial is created by adding to both sides of the equation, the square of half the coefficient of the linear term (the term whose variable is not squared). Note that you must account for the factored out value when adding the square of half the linear term to the other side of the equation. Then the perfect square trinomial is evaluated and then we solve for the variable to get the solution(s) to the quadratic equation.
Timestamps:
0:00 Intro
0:40 Start of Problem
Corrections:
9:51 I made a mistake, -21/2 multiplied with 1/6 is -21/12. Final answer: -1/2 plus/minus \sqrt(21/12i)
Organized Videos:
✅How to Solve a Quadratic by Completing the Square
✅Solve a Quadratic by Completing the Square | Fractions
✅Solve a Quadratic by Completing the Square | -x^2+bx+c
✅Solve a Quadratic by Completing the Square | 2x^2+bx+c
✅Solve a Quadratic by Completing the Square | ax^2+bx+c
✅Solve a Quadratic by Completing the Square | x^2+bx+c
✅Solve a Quadratic by Completing the Square | Learn About
Connect with me:
#Solvequadratics #completethesquare #brianmclogan
Комментарии
 0:10:03
0:10:03
 0:13:08
0:13:08
 0:03:39
0:03:39
 0:04:07
0:04:07
 0:01:15
0:01:15
 0:19:47
0:19:47
 0:24:12
0:24:12
 0:06:11
0:06:11
 0:02:25
0:02:25
 0:12:55
0:12:55
 0:19:08
0:19:08
 0:26:22
0:26:22
 0:18:12
0:18:12
 0:05:00
0:05:00
 0:01:15
0:01:15
 0:09:16
0:09:16
 0:10:01
0:10:01
 0:08:01
0:08:01
 0:01:52
0:01:52
 0:07:59
0:07:59
 0:15:38
0:15:38
 0:08:49
0:08:49
 0:01:00
0:01:00
 0:06:33
0:06:33