The Four Fundamental Subspaces and the Fundamental Theorem | Linear Algebra

Показать описание

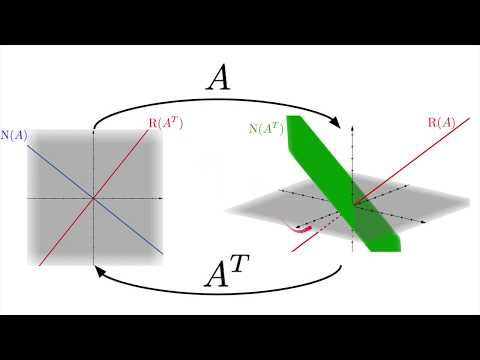
We introduce the four fundamental spaces associated with an mxn matrix A. These are the row space of A, the column space of A, the null space of A, and the null space of A transpose (also called the left null space of A). The row space and the null space of A are subspaces of R^n. The column space of A and the null space of A^T are subspaces of R^m. We'll then investigate the relationship between these spaces, and see how their dimensions can all be determined from the size of the matrix A and the rank of A. We then see that the fundamental spaces of the matrix come in orthogonal pairs, and in total we prove the fundamental theorem of linear algebra. #linearalgebra

Join Wrath of Math to get exclusive videos, lecture notes, and more:

0:00 Intro
0:34 Row Space, Column Space, and Null Space
1:38 The Four Fundamental Spaces
3:59 Subspaces of R^?
6:11 The Dimensions of the Subspaces
10:51 Spaces as Orthogonal Complements
19:25 The Fundamental Theorem of Linear Algebra
21:02 Conclusion

★DONATE★

Outro music by Ben Watts and is available for channel members.

Follow Wrath of Math on...

Рекомендации по теме

Комментарии

very ituitive explanation ever seen so far. Really good materials for newbies in LA. Recommended!

yizhu

Awesome video. There's a lot going on in a sentence like "the solutions to Ax=0 are the vectors in R^n that are orthogonal to every row vector of A." And it might not be obvious why the dot product is an effective demonstration of this.
It might help build some intuition for this by remembering that in 2D/3D space the dot product of two vectors shows the projection or shadow one vector casts on the other. Orthogonal vectors can't cast shadows on each other because they are perpendicular. Thus their dot product is zero and we can use Ax=0 to to find these vectors. These vectors are simultaneously the definition of the null space and orthogonal to the row vectors. Which is why we can say the null space and row space are orthogonal, and why the dot product is tool to get there.

jamesfehrmann

The Four Fundamental Subspaces and the Fundamental Theorem | Linear Algebra

04.2.1 Visualizing the Four Fundamental Spaces

Matrix Transpose and the Four Fundamental Subspaces

The Four Fundamental Subspaces and the Fundamental Theorem | Linear Algebra

The Four Fundamental Subspaces

Linear Algebra 21 : 4 Fundamental Subspaces

Computing the Four Fundamental Subspaces

Gilbert Strang: Four Fundamental Subspaces of Linear Algebra

Finding Bases for the Four Subspaces

04.2.1 The Four Fundamental Spaces

Problems on four fundamental subspaces - SS

Inverse matrices, column space and null space | Chapter 7, Essence of linear algebra

Four fundamental subspaces - SS

Null space and column space basis | Vectors and spaces | Linear Algebra | Khan Academy

04.3.1 SVD and the Four Fundamental Subspaces

#linearalgebra find bases and dimensions of the 4 fundamental subspaces

The Four Fundamental Subspaces: Part 1/5 'Fundamental Subspaces'

EAS205, 2014, Lecutre 12: Four fundamental subspaces

The Four Fundamental Subspaces: Part 2/5 'Examples'

Math 350 Mar 1st: Four subspaces (Video 1 of 3)

Dimensions of the four fundamental subspaces with examples

daglin 1075 first intro to the four fundamental subspaces any vector in space is sum of unique vect

Lecture 10: Dimensions of the Four Fundamental Subspaces

4 .1 Orthogonality of Four Fundamental Subspaces

3.5 the Four Fundamental Subspaces