filmov
tv
Computing the Four Fundamental Subspaces

Показать описание
MIT 18.06SC Linear Algebra, Fall 2011
Instructor: Ben Harris
A teaching assistant works through a problem on the four fundamental subspaces.
License: Creative Commons BY-NC-SA
Instructor: Ben Harris
A teaching assistant works through a problem on the four fundamental subspaces.
License: Creative Commons BY-NC-SA
Computing the Four Fundamental Subspaces
04.2.1 Visualizing the Four Fundamental Spaces
04.2.1 The Four Fundamental Spaces
Gilbert Strang: Four Fundamental Subspaces of Linear Algebra
Finding Bases for the Four Subspaces
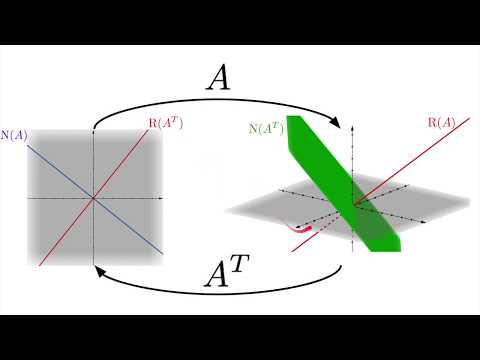
The Four Fundamental Subspaces
Problems on four fundamental subspaces - SS
3.5 the Four Fundamental Subspaces
#linearalgebra find bases and dimensions of the 4 fundamental subspaces
Lecture 10: Dimensions of the Four Fundamental Subspaces
Matrix Transpose and the Four Fundamental Subspaces
Four fundamental subspaces - SS
Lec11 - The Four Fundamental Subspaces: Applications to Graphs and Orthogonality
Inverse matrices, column space and null space | Chapter 7, Essence of linear algebra
EAS205, 2014, Lecutre 12: Four fundamental subspaces
10.3.3 Fundamental Subspaces Part 1
linalg14
Null space and column space basis | Vectors and spaces | Linear Algebra | Khan Academy
4.3.1 SVD and the Four Fundamental Subspaces
04.3.1 SVD and the Four Fundamental Subspaces
Dimensions of the four fundamental subspaces with examples
Finding Basis for Column Space, Row Space, and Null Space - Linear Algebra
The four fundamental subspacesand their application
Find bases for the four fundamental subspaces of the matrix A shown below. [ N(A)=… ]
Комментарии
 0:10:45
0:10:45
 0:02:41
0:02:41
 0:03:52
0:03:52
 0:06:04
0:06:04
 0:30:09
0:30:09
 0:12:00
0:12:00
 0:13:03
0:13:03
 0:39:53
0:39:53
 0:23:52
0:23:52
 0:52:54
0:52:54
 0:13:45
0:13:45
 0:18:01
0:18:01
 1:46:02
1:46:02
 0:12:09
0:12:09
 1:13:28
1:13:28
 0:07:32
0:07:32
 0:48:35
0:48:35
 0:25:13
0:25:13
 0:04:13
0:04:13
 0:04:13
0:04:13
 0:03:43
0:03:43
 0:18:31
0:18:31
 0:30:26
0:30:26
 0:00:33
0:00:33