filmov
tv
solving a HARD SAT big exponent equation the math way

Показать описание
-----------------------------
If you find my channel helpful and would like to support it 💪, then you can
-----------------------------
#justalgebra #SAT
solving a HARD SAT big exponent equation the math way
The Hardest Problem on the SAT📚 | Algebra | Math
The Hardest SAT Math Question is EASY!
Asking MIT students their SAT scores
Units Digit of 4 Math Trick Question | SAT Prep | JusticeTheTutor #math #maths #shorts
My Insane SAT Score Progression! #shorts
One of the HARDEST SAT Question | Which is bigger?
so you waited till last minute to study for the SAT...
[March SAT Math] How To Solve Every Question in SECONDS [Best Prep]
How to solve the hardest SAT question in 10 seconds!
The SAT Question Everyone Got Wrong
The hardest question on the 2024 SAT 🧐 (Note: this is a 45-45-90 triangle) #digitalsat #satprep
25 HARD SAT Math Problems
Solving Equations Algebra SAT Math Practice
SAT Math - Percentages Question
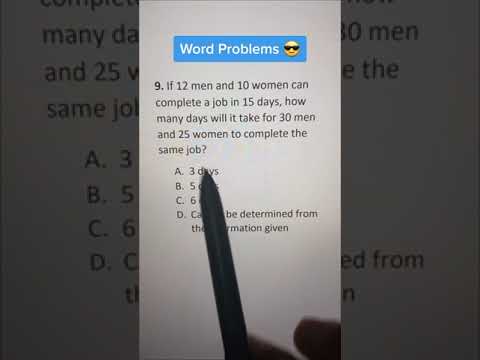
SAT Math - Word Problems Short Cuts
CRAZY HARD SAT Math Rates problem
One Of The Hardest SAT Math Problems - Can You Solve It In 2 Minutes?
A harder equation with exponents SAT Math Review
Do problem in seconds Hard SAT Math Trigonometry shortcut
The only SAT Math DESMOS Guide you'll ever need
Solving Exponential Equations without a calculator for the SAT Math
One of the MOST MISSED Equations and Question on the SAT
Solution of complicated Algebra Problem in a simple way | SAT tricks | YouTube Shorts
Комментарии
 0:04:32
0:04:32
 0:00:31
0:00:31
 0:00:35
0:00:35
 0:00:38
0:00:38
 0:00:31
0:00:31
 0:01:00
0:01:00
 0:08:06
0:08:06
 0:05:59
0:05:59
![[March SAT Math]](https://i.ytimg.com/vi/Q1kfnVJ32jM/hqdefault.jpg) 0:07:20
0:07:20
 0:00:31
0:00:31
 0:18:25
0:18:25
 0:00:46
0:00:46
 2:36:19
2:36:19
 0:00:43
0:00:43
 0:00:35
0:00:35
 0:00:42
0:00:42
 0:01:00
0:01:00
 0:04:41
0:04:41
 0:00:47
0:00:47
 0:01:00
0:01:00
 0:17:04
0:17:04
 0:00:59
0:00:59
 0:01:00
0:01:00
 0:00:20
0:00:20