filmov
tv
Basic Integration... How? (NancyPi)
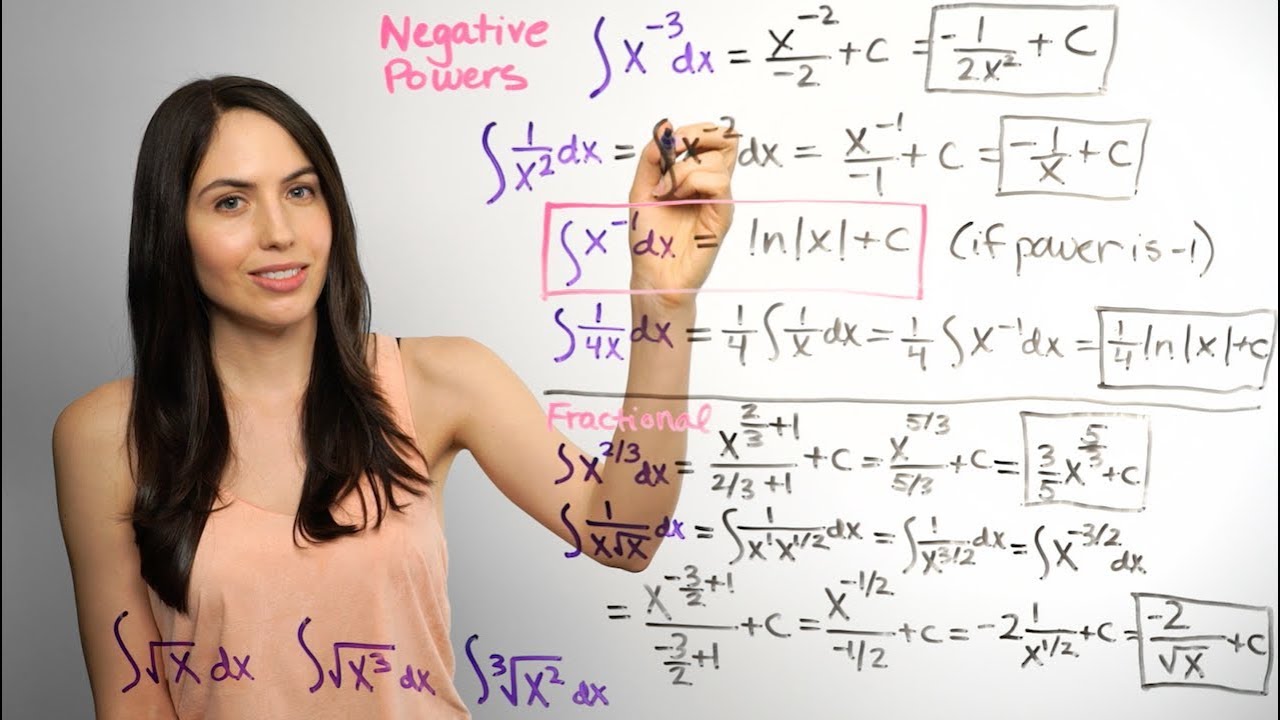
Показать описание
MIT grad shows how to find antiderivatives, or indefinite integrals, using basic integration rules. To skip ahead: 1) For how to integrate a polynomial with the POWER RULE, skip to 1:35. 2) For how to integrate NEGATIVE POWERS of x, FRACTIONAL POWERS of x, and RADICALS/ROOTS, skip to 6:12. 3) For how to integrate x^(-1), or 1/x, with the LOG RULE, skip to 7:23. 4) For examples where you use more algebra to rewrite before integrating, to SEPARATE the numerator of a FRACTION, or EXPAND a PRODUCT in order to use the Power Rule, skip to 10:00. 5) For basic TRIG and EXPONENTIAL examples that use rules from the Table of Integrals, as well as trig identities, skip to 11:36. Nancy formerly of MathBFF explains the steps.
1) POWER RULE: If you're integrating a polynomial, or just a power of x, you can use the Power Rule on each x-term in the polynomial. The Power Rule says that for a term that's just a power of x, such as x^3, you can integrate by raising the power by 1 AND dividing by that number (the new number you got by increasing the power by 1). For example, the integral of x^3 would be (x^4)/4. If there was a constant multiplied in front of the x-power, you can keep the constant and integrate the rest of the term (Constant Multiple Rule). For example, the integral of 6x^2 would be 6 times (x^3)/3, which simplifies to 2x^3. You can repeat these steps to integrate every term in the polynomial and string them together for the full integral. You can also keep the addition and subtraction between the terms (because of the Sum and Difference Rules). NOTE: The anti-derivative of a constant (just a number) is always that number times x (the Constant Rule), so the integral of 1 is 1*x, or x. At the end, it's very important to remember to add a constant of integration, to include a "+ c" at the end of your answer, when it is an indefinite integral (integral with no limits). ANOTHER NOTE: The Power Rule only works when the power is not -1.
2) NEGATIVE & FRACTIONAL POWERS, and RADICALS: For negative powers, you can still use the Power Rule, as long as the power is not -1. For fractional powers, you can also use the Power Rule. When you increase a fractional power by 1, you will have to simplify the power (before integrating) by getting a common denominator. For roots, like the square root of x, it's best to rewrite the radical as a fractional power, and then use the Power Rule.
3) IF THE X POWER IS -1 in the integrand, either written as x^(-1) or 1/x, you have to use a special rule, the LOG RULE, that you can find on a Table of Integrals. It says that the anti-derivative of x^(-1), or (1/x) is the natural log of the absolute value of x, plus c.
4) MORE ALGEBRA: Sometimes you may need to do a bit more algebra before integrating, so that the integrand is in a form that fits a basic integration rule, like the Power Rule. If you're integrating a rational expression, you can sometimes separate the numerator, or break the fraction into separate fractions, simplify each term, and then integrate with the Power Rule. If you have a product of x expressions, you can multiply it out, or distribute the factors so that you have just a polynomial (and can use the Power Rule).
5) TRIG & EXPONENTIAL: You can find a lot of trigonometric (and exponential) integral rules in the Table of Integrals. If you don't see it in the table, you may need to use a trig identity first, to rewrite the integrand into a form that you can integrate.
1) POWER RULE: If you're integrating a polynomial, or just a power of x, you can use the Power Rule on each x-term in the polynomial. The Power Rule says that for a term that's just a power of x, such as x^3, you can integrate by raising the power by 1 AND dividing by that number (the new number you got by increasing the power by 1). For example, the integral of x^3 would be (x^4)/4. If there was a constant multiplied in front of the x-power, you can keep the constant and integrate the rest of the term (Constant Multiple Rule). For example, the integral of 6x^2 would be 6 times (x^3)/3, which simplifies to 2x^3. You can repeat these steps to integrate every term in the polynomial and string them together for the full integral. You can also keep the addition and subtraction between the terms (because of the Sum and Difference Rules). NOTE: The anti-derivative of a constant (just a number) is always that number times x (the Constant Rule), so the integral of 1 is 1*x, or x. At the end, it's very important to remember to add a constant of integration, to include a "+ c" at the end of your answer, when it is an indefinite integral (integral with no limits). ANOTHER NOTE: The Power Rule only works when the power is not -1.
2) NEGATIVE & FRACTIONAL POWERS, and RADICALS: For negative powers, you can still use the Power Rule, as long as the power is not -1. For fractional powers, you can also use the Power Rule. When you increase a fractional power by 1, you will have to simplify the power (before integrating) by getting a common denominator. For roots, like the square root of x, it's best to rewrite the radical as a fractional power, and then use the Power Rule.
3) IF THE X POWER IS -1 in the integrand, either written as x^(-1) or 1/x, you have to use a special rule, the LOG RULE, that you can find on a Table of Integrals. It says that the anti-derivative of x^(-1), or (1/x) is the natural log of the absolute value of x, plus c.
4) MORE ALGEBRA: Sometimes you may need to do a bit more algebra before integrating, so that the integrand is in a form that fits a basic integration rule, like the Power Rule. If you're integrating a rational expression, you can sometimes separate the numerator, or break the fraction into separate fractions, simplify each term, and then integrate with the Power Rule. If you have a product of x expressions, you can multiply it out, or distribute the factors so that you have just a polynomial (and can use the Power Rule).
5) TRIG & EXPONENTIAL: You can find a lot of trigonometric (and exponential) integral rules in the Table of Integrals. If you don't see it in the table, you may need to use a trig identity first, to rewrite the integrand into a form that you can integrate.
Комментарии
 0:15:37
0:15:37
 0:25:48
0:25:48
 0:18:00
0:18:00
 0:06:05
0:06:05
 0:06:53
0:06:53
 0:14:30
0:14:30
 0:16:36
0:16:36
 0:07:15
0:07:15
 0:00:35
0:00:35
 0:32:52
0:32:52
 0:00:31
0:00:31
 0:11:56
0:11:56
 0:14:17
0:14:17
 0:12:48
0:12:48
 0:04:05
0:04:05
 0:11:05
0:11:05
 0:16:42
0:16:42
 0:19:15
0:19:15
 0:22:40
0:22:40
 0:00:33
0:00:33
 0:26:12
0:26:12
 0:14:13
0:14:13
 0:14:30
0:14:30
 0:11:13
0:11:13