filmov
tv
A beautiful combinatorical proof of the Brouwer Fixed Point Theorem - Via Sperner's Lemma

Показать описание
Using a simple combinatorical argument, we can prove an important theorem in topology without any sophisticated machinery.
Brouwer's Fixed Point Theorem: Every continuous mapping f(p) from between closed balls of the same dimension have a fixed point where f(p)=p.
Sperner's Lemma: Every Sperner covering of a triangulation - that is, unique colors on exterior vertices, edges inherent the colors between the vertices, and insides inherent any of the colors - contains at least one triangle with vertices of all three colors.
We require exactly no technical machinery to prove Sperner's Lemma. To prove Brouwer from Sperner we do need one major theorem, Bolzano-Weierstrauss, which shows the existence of convergent subsequences on closed and bounded regions.
Leave the proof of the general case for n greater than 2 in the comments!
BECOME A MEMBER:
MATH BOOKS & MERCH I LOVE:
Brouwer's Fixed Point Theorem: Every continuous mapping f(p) from between closed balls of the same dimension have a fixed point where f(p)=p.
Sperner's Lemma: Every Sperner covering of a triangulation - that is, unique colors on exterior vertices, edges inherent the colors between the vertices, and insides inherent any of the colors - contains at least one triangle with vertices of all three colors.
We require exactly no technical machinery to prove Sperner's Lemma. To prove Brouwer from Sperner we do need one major theorem, Bolzano-Weierstrauss, which shows the existence of convergent subsequences on closed and bounded regions.
Leave the proof of the general case for n greater than 2 in the comments!
BECOME A MEMBER:
MATH BOOKS & MERCH I LOVE:
Комментарии
 0:19:30
0:19:30
 0:03:42
0:03:42
 0:06:42
0:06:42
 0:06:57
0:06:57
 0:09:01
0:09:01
 0:11:44
0:11:44
 0:08:12
0:08:12
 0:03:22
0:03:22
 0:08:59
0:08:59
 0:05:37
0:05:37
 0:03:57
0:03:57
 0:00:55
0:00:55
 0:47:51
0:47:51
 1:16:21
1:16:21
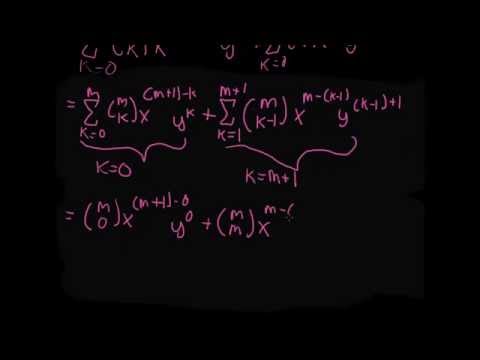 0:15:44
0:15:44
 0:13:12
0:13:12
 0:03:29
0:03:29
 0:00:48
0:00:48
 0:05:43
0:05:43
 0:04:34
0:04:34
 0:06:36
0:06:36
 0:10:19
0:10:19
 0:06:55
0:06:55
 0:06:12
0:06:12