filmov
tv
Binomial Theorem Proof by Induction

Показать описание
Talking math is difficult. :)
Here is my proof of the Binomial Theorem using indicution and Pascal's lemma. This is preparation for an exam coming up.
Please let me know if I made any errors.
Here is my proof of the Binomial Theorem using indicution and Pascal's lemma. This is preparation for an exam coming up.
Please let me know if I made any errors.
The Binomial Theorem Proof by Induction
Binomial Theorem || Proof by Mathematical Induction
Binomial Theorem Proof by Induction
Induction with Sigma Notation (3 of 4: Binomial Theorem - completing proof)
Ext2: Mathematical Induction (Proof by Binomial Theorem)
How to prove Binomial Theorem by Induction
Binomial theorem: Proof by Induction Lecture 6
Binomial Theorem Proof | Proof by Induction | Mathematiks
Proving the Binomial Theorem using Mathematical Induction
Binomial Theorem- Proof using Induction
Mathematical Induction Practice Problems
Binomial expansion proof by induction
An ingenious & unexpected proof of the Binomial Theorem (1 of 2: Prologue)
Proving Binomial Theorem by Mathematical Induction
Proving the Binomial Theorem | Induction |
Combinatorial Proof of Binomial Theorem
State and prove BINOMIAL THEOREM using principle of mathematical induction.
Proof of The Binomial Theorem
Induction with Sigma Notation (2 of 4: Binomial Theorem - setting up proof)
Induction with Sigma Notation (4 of 4: Binomial Theorem - Pascal's Identity)
Binomial Theorem - Proof by Mathematical Induction
Proof by induction | Sequences, series and induction | Precalculus | Khan Academy
Extension 2 Exam Review (7 of 7: Binomial Theorem / Induction Proof)
Binomial Expansion Proof By Mathematical Induction Process
Комментарии
 0:06:36
0:06:36
 0:15:48
0:15:48
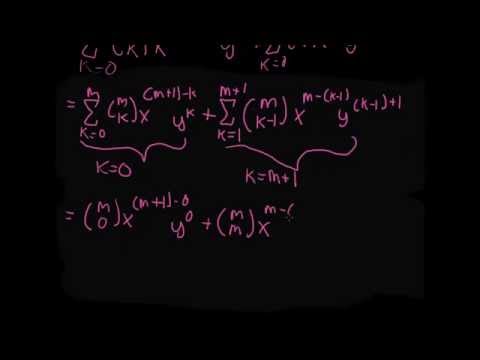 0:15:44
0:15:44
 0:18:03
0:18:03
 0:15:48
0:15:48
 0:06:27
0:06:27
 0:05:04
0:05:04
 0:14:05
0:14:05
 0:11:23
0:11:23
 0:02:33
0:02:33
 0:18:08
0:18:08
 0:18:33
0:18:33
 0:06:55
0:06:55
 0:08:59
0:08:59
 0:21:08
0:21:08
 0:04:57
0:04:57
 0:16:06
0:16:06
 0:17:55
0:17:55
 0:08:02
0:08:02
 0:08:47
0:08:47
 0:17:47
0:17:47
 0:09:23
0:09:23
 0:09:14
0:09:14
 0:08:09
0:08:09