filmov
tv
Poland Math Olympiad | A Very Nice Geometry Problem

Показать описание
Poland Math Olympiad | A Very Nice Geometry Problem
MY OTHER CHANNELS
••••••••••••••••••••••••••••••••
--------------------------------------------------------------------------------
Join the channel to become a member
MY OTHER CHANNELS
••••••••••••••••••••••••••••••••
--------------------------------------------------------------------------------
Join the channel to become a member
Poland Math Olympiad | A Very Nice Geometry Problem
Poland| A nice algebra problem #maths#olympiad
Poland Math Olympiad | A Very Nice Geometry Problem
Poland Math Olympiad | A Very Nice Geometry Problem
A Nice and Symmetric Equation | Polish Mathematical Olympiad Second Round
Poland Math Olympiad Problem
An Olympiad Problem from Poland 🇵🇱
Poland Math Olympiad | A Very Nice Geometry Problem | 2 Different Methods
Poland | A Nice Algebra Problem | Math Olympiad
An Arithmetic Puzzle from Polish Mathematical Olympiads
Poland | A Nice Algebra Problem | Math Olympiad
A Nice Trick to Degenerate This Equation Instantly | Polish Maths Olympiad Finals 2013
Polish Math Olympiad | 2017
Poland - Math Olympiad Question | You should be able to solve this!
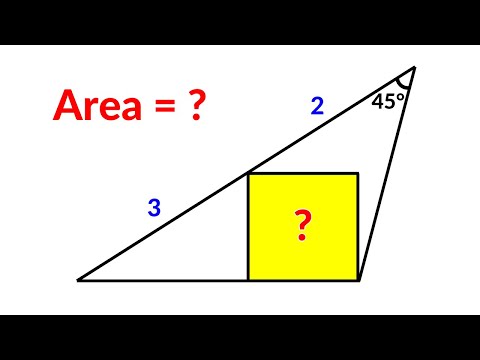
Poland Math Olympiad | A Very Nice Geometry Problem
Polish Mathematical Olympiad | Olympiad training problems
Polish Mathematical Olympiad, 2nd round, 1992/1993, problem 6
Poland Math Olympiad | A Very Nice Geometry Problem
amazing Polish Mathematical olympiad
Poland - Math Olympiad Question | You should be able to solve this!
Olympiad Mathematics | Algebra Problem | Poland Junior Math Olympiad | Math Problems
Integers Unleashed: Polish Math Olympiad Problem
Poland Math Olympiad Problem | A Nice Challenge of Number Theory
Poland - Math Olympiad Question | You Should be able to Solve ??
Комментарии
 0:11:13
0:11:13
 0:07:27
0:07:27
 0:13:08
0:13:08
 0:13:29
0:13:29
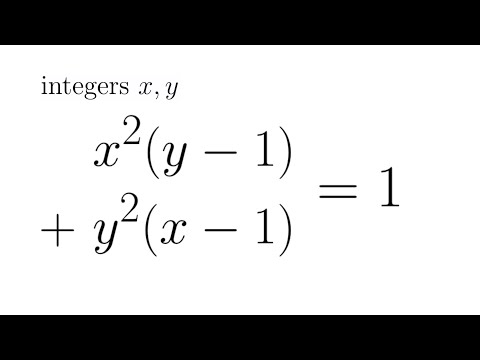 0:07:35
0:07:35
 0:05:32
0:05:32
 0:10:39
0:10:39
 0:17:18
0:17:18
 0:09:08
0:09:08
 0:05:57
0:05:57
 0:15:15
0:15:15
 0:09:31
0:09:31
 0:10:21
0:10:21
 0:00:50
0:00:50
 0:11:35
0:11:35
 0:02:42
0:02:42
 0:05:05
0:05:05
 0:12:12
0:12:12
 0:10:07
0:10:07
 0:00:51
0:00:51
 0:03:27
0:03:27
 0:11:37
0:11:37
 0:08:24
0:08:24
 0:00:36
0:00:36