filmov
tv
A Nice and Symmetric Equation | Polish Mathematical Olympiad Second Round
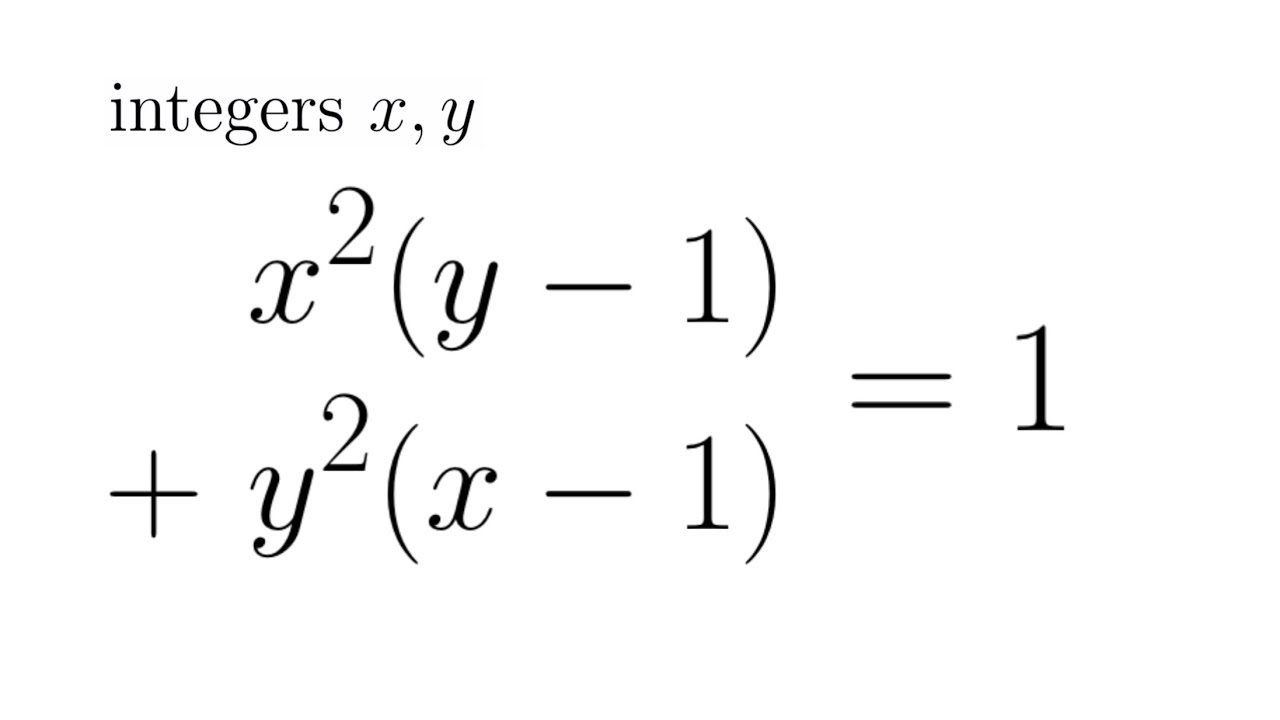
Показать описание
How To Find The Vector Equation of a Line and Symmetric & Parametric Equations
A Nice and Symmetric Equation | Polish Mathematical Olympiad Second Round
Symmetric Equation Q10
Symmetric Equations - Lines in Space
Determine Vector, Parametric and Symmetric Equation of Line from Two Points
Parametric and symmetric equations of the line (KristaKingMath)
SYSTEM OF SYMMETRIC EQUATIONS
Vector Equation, Parametric Equations and Symmetric Equation Passing Through Two Points (3D)
Visual Algebra, Lecture 2.6: Symmetric and alternating groups
Write Vector and Symmetric Equation of Lines Q6
A Beautiful and Symmetric Inequality
System of Symmetric Equations
A Nice Symmetric System of Equations | Baltic Way 2021
How to Write Symmetric Equation in Vector Form
🔶09 - Vector, Parametric and Symmetric Equations of a line in a 3D-plane: Ex1 and Ex2
How to Find the Parametric and Symmetric Equations of a Line Given Two Points in Space
A 'symmetric' system of equations.
A Symmetric Equation: a / b^2 + b / a^2 = 1/a + 1/b || High School Math
Fractional Equations and system of symmetric equations
a symmetric system of equations from El Salvador
Example of Symmetric Equations of a Line
Given Two Points on a Line Find the Parametric and Symmetric Equations
Vectors - Vector, Parametric and Symmetric Equations of Lines
Problem on Symmetric equation
Комментарии
 0:11:37
0:11:37
 0:07:35
0:07:35
 0:03:03
0:03:03
 0:03:21
0:03:21
 0:05:03
0:05:03
 0:08:44
0:08:44
 0:08:46
0:08:46
 0:05:17
0:05:17
 0:52:57
0:52:57
 0:05:43
0:05:43
 0:07:03
0:07:03
 0:08:19
0:08:19
 0:11:49
0:11:49
 0:03:25
0:03:25
 0:24:50
0:24:50
 0:08:59
0:08:59
 0:07:38
0:07:38
 0:06:02
0:06:02
 0:05:13
0:05:13
 0:12:23
0:12:23
 0:02:49
0:02:49
 0:05:18
0:05:18
 0:05:48
0:05:48
 0:00:47
0:00:47