filmov
tv
A Nice Trick to Degenerate This Equation Instantly | Polish Maths Olympiad Finals 2013
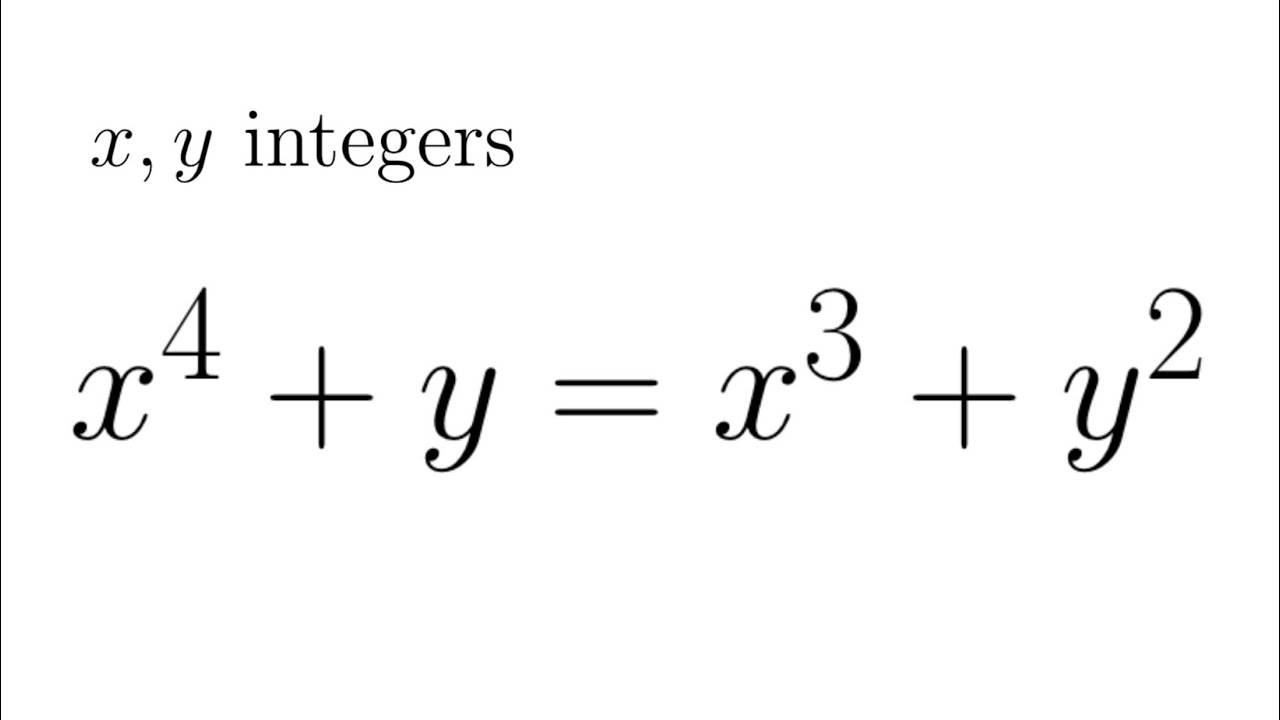
Показать описание
A Nice Trick to Degenerate This Equation Instantly | Polish Maths Olympiad Finals 2013
SPOKEN LIKE A TRUE DEGENERATE 😛
THE FITNESS WORLDS BIGGEST DEGENERATE! 😂
The BEST NoFap Strategy
Degenerate activities 😈
Plans are only good intentions unless they immediately degenerate into hard work. #mindset #shots
Degenerate Weeb Spots A Nice View At Katsucon 2020...
Plans are only good intentions unless they immediately degenerate into hard work.-Peter Drucker
Send this to your degenerate…
SNIFF IT BABY🔥😆 #callofdutymw2 #degenerate #funnyshorts #mw2 #codclips
Signs you're a degenerate man (feat. Jordan Peterson AI)
I’m a degenerate
'A Degenerate Murderer' 🥶 #shorts #reddeadredemption #edit #rdr2 #viral #arthurmorgan #due...
Degenerate Gambler Dana White On How He Wins At Blackjack😳
STARSET - DEGENERATE (Official Lyric Video)
u can be a great student and a degenerate
Pokemon Degenerate Reacts to Furrymon by the Chalkeaters #shorts #pokemon
One day at a time lol!! #degeneracy #midlifevibes #midlifecoach #atwork #degenerate
Being a degenerate helps you win chess games #shorts
HAVE YALL PRESAVED MY DEBUT EP “Queen Degenerate” YET ? 🐷🥺⭐️💖❄️🌱💵 #hyperpop #dancevideo #dance...
STARSET - DEGENERATE (Official Music Video)
Degenerate Art - Unfettered Creativity
'𝗣𝗹𝗮𝗻𝘀 𝗮𝗿𝗲 𝗼𝗻𝗹𝘆 𝗴𝗼𝗼𝗱 𝗶𝗻𝘁𝗲𝗻𝘁𝗶𝗼𝗻𝘀 𝘂𝗻𝗹𝗲𝘀𝘀 𝘁𝗵𝗲𝘆 𝗶𝗺𝗺𝗲𝗱𝗶𝗮𝘁𝗲𝗹𝘆 𝗱𝗲𝗴𝗲𝗻𝗲𝗿𝗮𝘁𝗲 𝗶𝗻𝘁𝗼 𝗵𝗮𝗿𝗱 𝘄𝗼𝗿𝗸.' -𝙋𝙚𝙩𝙚𝙧...
Fatui Edit || Genshin Impact | Degenerate
Комментарии
 0:09:31
0:09:31
 0:00:33
0:00:33
 0:00:20
0:00:20
 0:06:57
0:06:57
 0:00:16
0:00:16
 0:00:09
0:00:09
 0:00:05
0:00:05
 0:00:06
0:00:06
 0:00:12
0:00:12
 0:00:06
0:00:06
 0:00:17
0:00:17
 0:00:10
0:00:10
 0:00:24
0:00:24
 0:00:20
0:00:20
 0:03:37
0:03:37
 0:00:10
0:00:10
 0:00:27
0:00:27
 0:00:07
0:00:07
 0:01:00
0:01:00
 0:00:30
0:00:30
 0:03:42
0:03:42
 0:03:37
0:03:37
 0:00:09
0:00:09
 0:00:25
0:00:25