filmov
tv
Spinors for Beginners 14: Minimal Left Ideals (and Pacwoman Property)

Показать описание
0:00 - Introduction
2:01 - Review of Cl(3,0)
4:28 - Fitting Spinors into Cl(3,0)
8:09 - Minimal Left Ideals
11:39 - Projectors
12:55 - Pacwoman Property
14:17 - Calculating Minimal Left Ideal in Cl(3,0)
17:45 - Spin Operators in Cl(3,0)
19:35 - Dual Spinors and Inner Product
24:40 - Spinor Outer Product
27:20 - Hestenes Definition of Spinors
30:18 - Generalizing to Cl(1,3)
37:10 - Generalizing to Cl(p,q)
41:00 - Faithful Matrix Representations
Spinors for Beginners 14: Minimal Left Ideals (and Pacwoman Property)
Spinors for Beginners 1: Introduction (Overview +Table of Contents for video series)
Spinors for Beginners 15: Nilpotents, Fermions, and Maximally Isotropic Subspaces
Spinors for Beginners 9: Pauli Spinors vs Weyl Spinors vs Dirac Spinors
Spinors for Beginners 13: Ideals and Projectors (Idempotents)
Spinors for Beginners 11: What is a Clifford Algebra? (and Geometric, Grassmann, Exterior Algebras)
Spinors for Beginners 3: Polarizations and SU(2) Matrices [and O(3), SO(3), U(2)]
Spinors, ideals, and algebraic black holes (Video 5/14).
Spinors for Beginners 8: Are the Pauli Matrices also Vectors? (Intro to Spinor Spaces)
Spinors for Beginners 12: How the Spin Group Generalizes Quaternions to any Dimension
Spinors for Beginners 5: The Flagpole and Complex Projective Line (CP1)
Weyl spinors as ideals of the complex quaternions (Video 6/14).
Introduction to Mathematics of Spinors (from a self-learner)
Spinor Lorentz Transformations | How to Boost a Spinor
His reaction when he sees her FEET for the first time…😳 #Shorts
Spinor model as a position coordinate function
Intro to Spinors 1
Solutions of the Dirac Equation
spinors
Summary (Video 13/14).
Quarks and leptons as ideals of the Clifford algebra CL(6) (Video 11/14)
Spinning Spinors (SU(2) Rotations)
How the complex quaternions give each of the Lorentz reps of the standard model (Video 7/14)
Spinor
Комментарии
 0:42:07
0:42:07
 0:18:59
0:18:59
 0:27:06
0:27:06
 0:46:07
0:46:07
 0:26:11
0:26:11
 0:33:23
0:33:23
 0:24:16
0:24:16
 0:02:14
0:02:14
 0:24:08
0:24:08
 0:47:16
0:47:16
 0:24:24
0:24:24
 0:05:22
0:05:22
 0:07:05
0:07:05
 0:03:07
0:03:07
 0:01:00
0:01:00
 0:00:04
0:00:04
 0:22:31
0:22:31
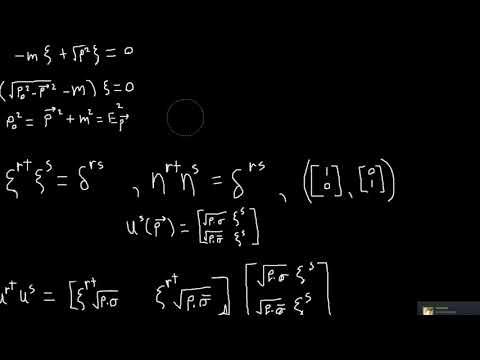 0:07:55
0:07:55
 0:06:23
0:06:23
 0:06:04
0:06:04
 0:08:41
0:08:41
 0:17:45
0:17:45
 0:04:16
0:04:16
 0:20:16
0:20:16